Das Summenzeichen und die Streifenmethode
Wir wollen versuchen die Fläche zwischen 
und der x-Achse von der senkrechten Geraden x = 0 bis zur senkrechten Geraden x = b zu berechnen. Zu Beginn werden wir mit b = 8 rechnen;erst später werden wir mit der allgemeinen oberen Grenze b arbeiten.
Wir suchen jetzt also die Fläche A zwischen der Normalparabel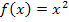 
, den Koordinatenachsen und der Geraden x = 8. In anderen Worten:Es ist das bestimmte Integral 
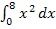gesucht. Vergleiche Abb. 1!
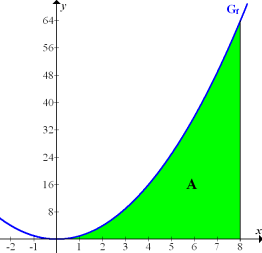
Abb. 1:Graph 
der Normalparabel 
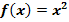mit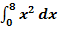 
(grün markierte Fläche A)
Um den Inhalt der Fläche A näherungsweise zu berechnen, werden wir die Fläche A in Streifen gleicher Breite 
einteilen und dann jeweils Ober- und Untersumme berechnen. Zuerst werden wir dies mit nur 2 Streifen machen. Der exakte Wert des Flächeninhalts liegt dabei zwischen dem Ergebnis der Obersumme und dem der Untersumme. Ein Näherungswert für A ergibt sich aus dem Durchschnitt der beiden Ergebnisse. Diese Abschätzung ist natürlich noch sehr ungenau. Daher werden wir nach und nach die Anzahl n der Streifen erhöhen;wir werden dann mit 4 und 8 Streifen arbeiten. Um den exakten Inhalt der Fläche A zu erhalten, müsste man die Anzahl n der Streifen gegen Unendlich gehen lassen. Diese Berechnung werden wir für b = 8 nicht durchführen. Das heben wir uns für die Berechnungen mit der allgemeinen oberen Grenze b auf.
Näherungsweise zu berechnen: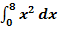
Es gilt somit:
Untere Grenze a = 0, obere Grenze b = 8 und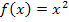
1. Näherung mit der Streifenanzahl n = 2
Berechnung der Obersumme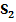 
:
Die Streifenbreite ergibt sich aus der Intervallbreite b – a = 8 – 0 = 8 und der Anzahl n (hier n = 2) der Streifen: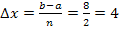 
Dass bei 2 Streifen im Intervall von 0 bis 8 für die Streifenbreite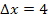 
gilt, erkennt man auch direkt an der nachfolgenden Abbildung. Beide Streifen haben die Breite .
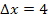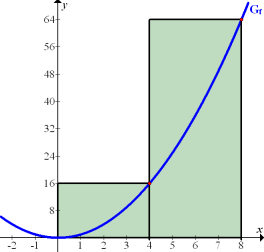
Abb. 2:Zur Berechnung der Obersumme 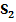im Intervall 0 bis 8 mit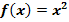
Bei der Obersumme wird in jedem Streifen von der y-Koordinate des Kurvenpunktes von 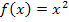ausgegangen, der am höchsten liegt. Da der Graph von 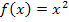für positive Werte von x streng monoton steigend ist, liegen die Kurvenpunkte mit der jeweils höchsten y-Koordinate immer am rechten Rand der Streifen. Die Punkte sind in der Abb. 2 rot markiert. Die y-Koordinaten dieser Punkte entsprechen jeweils der Höhe der rechteckigen Streifen. Bekanntlich berechnet man die Fläche eines Rechtecks nach der Formel „Länge mal Breite“, hier also „Streifenbreite mal Höhe“. Die Streifenbreite 
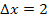ist bei beiden Rechtecken gleich, da wir das so festgelegt haben.
