Das Summenzeichen und die Streifenmethode
D.h. wir müssen das Integral 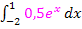 vom Integral
vom Integral 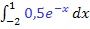 abziehen.
abziehen.
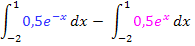
Diese beiden Integrale lassen sich zu einem Integral zusammenfassen, da sie beide die gleichen Grenzen haben.
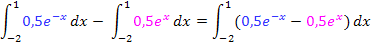
Tipp:Die Fläche zwischen zwei Funktionen entspricht immer dem Integral der Differenz beider Funktionen, wobei von der oben liegenden Funktion die unten liegende abgezogen werden muss.
Wir legen fest:
 ist die Funktion, welche die Fläche oben begrenzt.
ist die Funktion, welche die Fläche oben begrenzt.
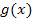 ist die Funktion, welche die Fläche unten begrenzt.
ist die Funktion, welche die Fläche unten begrenzt.
Dann wird die Fläche, welche im Intervall von a bis b (wobei gilt:a <b) zwischen beiden Funktionsgraphen liegt, mit dem folgenden Integral berechnet:
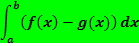
Diese Formel gilt übrigens auch dann, wenn die Funktionen  und
und 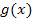 nicht positivwertig sind. Die Fläche zwischen den zwei Funktionen kann also auch komplett oder zumindest teilweise unterhalb der x-Achse liegen. Egal, wie die Fläche zur x-Achse liegt;die Formel stimmt grundsätzlich. Man muss nur darauf achten, dass man von der kleineren zur größeren Grenze integriert und das Integral „obere Funktion minus untere Funktion“ rechnet.
nicht positivwertig sind. Die Fläche zwischen den zwei Funktionen kann also auch komplett oder zumindest teilweise unterhalb der x-Achse liegen. Egal, wie die Fläche zur x-Achse liegt;die Formel stimmt grundsätzlich. Man muss nur darauf achten, dass man von der kleineren zur größeren Grenze integriert und das Integral „obere Funktion minus untere Funktion“ rechnet.
Nun zurück zum Integral 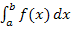 und zur Streifenmethode. Du hast inzwischen hoffentlich soweit verstanden, was ein bestimmtes Integral
und zur Streifenmethode. Du hast inzwischen hoffentlich soweit verstanden, was ein bestimmtes Integral 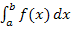 ist. Bloß, wie man es berechnen kann, haben wir noch nicht genau besprochen. Wie funktioniert nun die Streifenmethode? Wann wird sie angewendet?
ist. Bloß, wie man es berechnen kann, haben wir noch nicht genau besprochen. Wie funktioniert nun die Streifenmethode? Wann wird sie angewendet?
 |
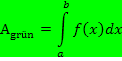
|
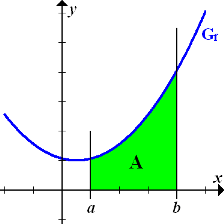
Es soll das bestimmte Integral 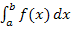 einer positivwertigen Funktion, also der Inhalt der Fläche A zwischen
einer positivwertigen Funktion, also der Inhalt der Fläche A zwischen  und der x-Achse von a bis b ausgerechnet werden. Solange
und der x-Achse von a bis b ausgerechnet werden. Solange  eine lineare Funktion (Gerade) ist, kann man sich mit den Formeln für den Inhalt von Dreieck oder Trapez behelfen. Bei linearen Funktionen braucht man daher die Streifenmethode nicht unbedingt. Doch was tun, wenn der Graph von
eine lineare Funktion (Gerade) ist, kann man sich mit den Formeln für den Inhalt von Dreieck oder Trapez behelfen. Bei linearen Funktionen braucht man daher die Streifenmethode nicht unbedingt. Doch was tun, wenn der Graph von  wie in der Abbildung eine Kurve ist? Genau dann brauchen wir die Streifenmethode.
wie in der Abbildung eine Kurve ist? Genau dann brauchen wir die Streifenmethode.
Grundgedanke der Streifenmethode:
Wir teilen die gesuchte Fläche A in Streifen gleicher Breite ein. Für kleine Streifenbreiten lässt sich damit die tatsächlich gesuchte Fläche A durch die Fläche von vielen kleinen Rechtecken näherungsweise berechnen.
Die Rechtecke sind dabei entweder ein wenig größer oder ein wenig kleiner als die gesuchte Fläche A, je nachdem ob man die Rechtecke alle oberhalb oder alle unterhalb des Graphen  einzeichnet.
einzeichnet.
Die Summe der zu großen Rechtecksflächen bezeichnen wir als Obersumme S. Bei der Obersumme geht man immer vom höchsten Kurvenpunkt innerhalb des jeweiligen Streifens aus, um die Höhe des jeweiligen Streifens zu erhalten.

