Das Summenzeichen und die Streifenmethode

(Wie die Sinusfunktion aussieht, weißt du hoffentlich:Sie verläuft durch den Ursprung und wiederholt sich periodisch nach 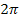. Ihre Nullstellen liegen immer bei den ganzzahligen Vielfachen von 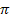.) Du musst nur die Sinusfunktion um 1 nach oben verschieben und schon hast du den Graph der Integrandenfunktion.

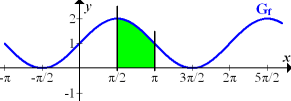
Abb.:Zum Integral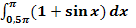

3. Bsp.:

In den folgenden Abbildungen ist jeweils eine Fläche farbig markiert. Gib jeweils das zugehörige Integral an!

Abb. 1

Abb. 2

Abb. 3

Lösung:

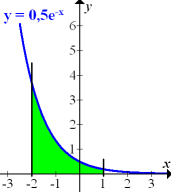
Die in Abb. 1 grün markierte Fläche liegt zwischen dem Graph der Funktion 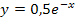und der x-Achse. Das bedeutet, dass 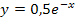die Integrandenfunktion ist. Du musst also 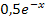hinter das Integralzeichen schreiben. Achtung:dx nicht vergessen! Die in Abb. 1 markierte Fläche wird links durch die senkrechte Gerade x = -2 und rechts durch die senkrechte Gerade x = 1 begrenzt. Die Grenzen des Integrals sind somit -2 und 1. Die Fläche liegt komplett oberhalb der x-Achse. Daher entspricht die Fläche dem folgenden Integral:

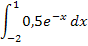
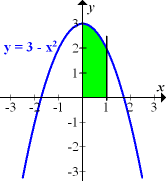
Die in Abb. 2 grün markierte Fläche liegt zwischen dem Graph der Funktion 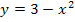und der x-Achse. Sie wird links durch die y-Achse begrenzt, welche die Gleichung x = 0 hat, und rechts durch die senkrechte Gerade x = 1. Die untere Grenze ist daher 0 und die obere Grenze 1. Die Fläche liegt komplett oberhalb der x-Achse. Daher entspricht die Fläche dem folgenden Integral:

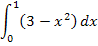
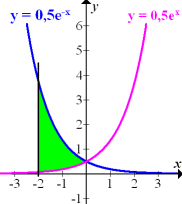
Die in Abb. 3 grün markierte Fläche liegt zwischen den Graphen der Funktionen 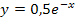und 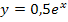. Sie wird links durch die senkrechte Gerade x = -2 und rechts durch die y-Achse begrenzt, welche die Gleichung x = 0 hat. Die Grenzen sind also -2 und 0. Das dürfte dir noch klar sein. Aber wie kann man nun diese Fläche durch ein Integral ausdrücken, obwohl sie gar nicht zwischen einer Funktion und der x-Achse liegt?

Wir betrachten die Graphen der beiden Funktionen einzeln. Der blaue Graph (gehört zu 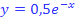) begrenzt die Fläche nach oben hin. Das Integral 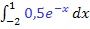entspricht der Fläche zwischen dem blauen Graph und der x-Achse von -2 bis 0. Dies ist aber noch nicht die in Abb. 3 grün markierte Fläche. Der rosa Graph (gehört zu 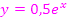)  begrenzt die grüne Fläche nach unten hin. Das Integral 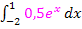entspricht der Fläche zwischen dem rosa Graph und der x-Achse. (Dies ist die kleine weiße Fläche zwischen x-Achse und der grünen Fläche von -2 bis 0.)

Vom Integral 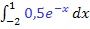muss man dann die Fläche abziehen, die im Bereich von -2 bis 0 zwischen dem rosa Graph und der x-Achse liegt.

---