Das Summenzeichen und die Streifenmethode

Wir halten fest:Nur bei positivwertigen Funktionen entspricht das bestimmte Integral 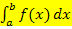der Fläche A zwischen 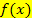und der x-Achse im Intervall [a;b]. Zumindest im Bereich zwischen a und b soll der Graph der Funktion nicht unterhalb der x-Achse verlaufen. Für x [a;b] soll also gelten: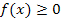

Nur unter den Voraussetzungen 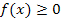und a <b entspricht das Ergebnis von 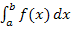dem Flächeninhalt A zwischen und der x-Achse im Intervall [a;b].

Obwohl wir noch gar nicht besprochen haben, wie man Integrale ausrechnet, können wir schon die einige Aufgaben zum Thema „Integral“ lösen. Wie solche Aufgaben aussehen können, siehst du auch an den zwei folgenden Beispielen. In diesen Beispielen geht es nur darum, die Integralschreibweise zu üben, noch nicht um die Berechnung der Integrale.

2. Bsp.:

Stelle folgende Integrale anschaulich dar!

a.)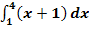

b.)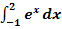

c.)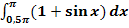

Lösung:

Wir müssen jeweils den Graph der Integrandenf unktion – das ist die Funktion, die zwischen dem Integralzeichen und dx steht – in ein Koordinatensystem zeichnen und die Fläche zwischen Graph und x-Achse im Bereich von a bis b markieren. Dabei ist a die untere Grenze des Integrals (d.h. die Zahl unten am Integralzeichen) und b die obere Grenze (d.h. die Zahl oben am Integralzeichen).

Zu 2a.)

Beim Integral 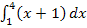ist die Integrandenfunktion: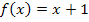

Der Graph von 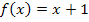ist eine Gerade mit der Steigung m = 1 und dem y-Achsenabschnitt t = 1. Die Funktionsgleichung hat schließlich die Form . (Ausführlichere Erklärungen bei:Geraden zeichnen) Wir zeichnen die Gerade 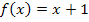mit Hilfe des y-Achsenabschnitts t = 1 und einem Steigungsdreieck (wegen m = 1 geht man 1 nach rechts und 1 nach oben) in ein Koordinatensystem. Dann markieren wir die Fläche zwischen und x-Achse von 1 bis 4. Sie liegt komplett oberhalb der x-Achse. Die markierte Fläche entspricht daher dem gesuchten Integral .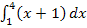

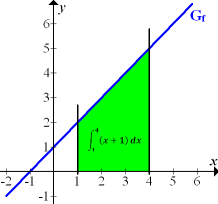
Abb.:Zum Integral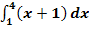

Zu 2b.)

Graphisch darzustellen:

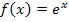Wir zeichnen den Graph der Integrandenfunktion in ein Koordinatensystem und markieren die Fläche zwischen und der x-Achse von -1 bis 2. Die Fläche liegt komplett oberhalb der x-Achse;sie entspricht deshalb .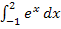

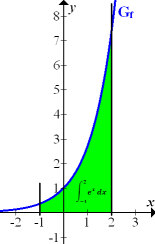
Abb.:Zum Integral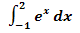

Zu 2c.)

Anschaulich darzustellen: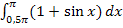

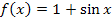Wir zeichnen den Graph der Integrandenfunktion in ein Koordinatensystem und markieren die Fläche zwischen und der x-Achse von 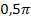bis .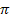

Hinweis:Den Graph der Integrandenfunktion 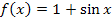erhält man durch Verschiebung des Graphen der Sinusfunktion 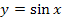um 1 nach oben.

---