Das Summenzeichen und die Streifenmethode
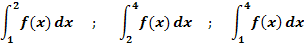
Lösung:
Gegeben sind die Flächeninhalte des rosa und des grünen Flächenstücks: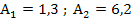 
Bei allen drei gesuchten Integralen ist die untere Grenze kleiner als die obere. Wir integrieren hier also immer in die „richtige“ Richtung. Somit zählt das Flächenstück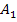 
bei der Flächenbilanz, d.h. beim Integral positiv, weil es oberhalb der x-Achse liegt. Das unterhalb der x-Achse liegende Flächenstück 
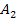zählt negativ bei der Flächenbilanz, also beim Integral, da wir von der kleineren zur größeren Zahl integrieren.
Geg.: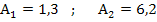 
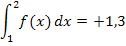
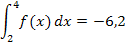
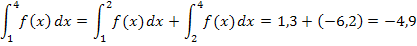
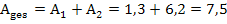
Du siehst daran, dass bei dem oberhalb der x-Achse liegenden Flächenstück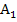 
das Integral 
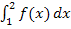wirklich der Fläche zwischen 
und der x-Achse von 1 bis 2 entspricht. Das Integral ist positiv und entspricht der Fläche .
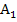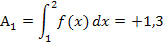
Bei dem unterhalb der x-Achse liegenden Flächenstück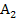 
sieht es anders aus:Das Integral 
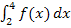entspricht nicht der Fläche von 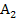, weil das Integral einen negativen Wert hat. Ein Flächeninhalt kann dagegen gar nicht negativ sein.
Du müsstest den Betrag des Integrals verwenden oder die Grenzen vertauschen, um wirklich den (positiven) Flächeninhalt von 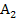zu erhalten.
Die Gesamtfläche beider gefärbter Flächenstücke zusammen entspricht ebenfalls nicht einfach dem Integral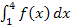 
, da ein Teil der Fläche unterhalb der x-Achse liegt.
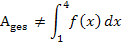
Das Integral 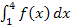entspricht hier nur der Flächenbilanz, nicht aber der Gesamtfläche zwischen Graph und x-Achse von 1 bis 4. Das Ergebnis 
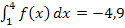lässt erkennen, dass die Fläche unterhalb der x-Achse zwischen Graph und x-Achse um 4,9 FE größer ist als die Fläche oberhalb der x-Achse.
Soll man die Gesamtfläche mittels Integralen berechnen, muss das Integral 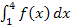an der Nullstelle von 
aufgeteilt werden. Diese Nullstelle liegt offensichtlich bei x = 2. Wir brauchen also die einzelnen Integrale 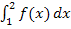und 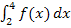, wobei um das Integral 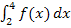unbedingt ein Betrag gesetzt werden muss, weil dieses Integral ohne Betrag einen negativen Wert liefert. Der Betrag von 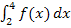muss dann noch zu dem ohnehin positiven Integral 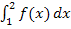addiert werden.
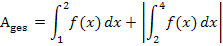
An diesem Beispiel ist dir hoffentlich klar geworden, dass das bestimmte Integral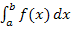 
nicht immer mit der Fläche zwischen und der x-Achse im Intervall [a;b] gleichzusetzen ist.
Zur Vereinfachung gehen wir allerdings im Folgenden davon aus, dass die gesuchte Fläche A komplett oberhalb der x-Achse liegt. Verläuft der Graph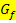 
vollständig oberhalb der x-Achse, sind alle Funktionswerte 
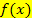positiv. Man nennt so eine Funktion „positivwertig“. Wir behandeln im Folgenden ausschließlich Integrale positivwertiger Funktionen.
