Das bestimmte und das unbestimmte Integral
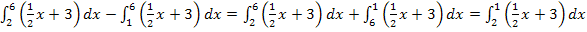
Es ergibt sich dabei zwar ein Integral, dessen obere Grenze kleiner ist als die untere, doch das macht nichts. Du musst dich beim Ausrechnen des Integrals nur grundsätzlich an die Regel „obere Grenze minus untere“ halten. Dann kommt auch das Richtige heraus.
Anschaulich kann man diese Zusammenhänge folgendermaßen interpretieren:
Die Funktion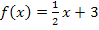 
ist eine Gerade mit der Steigung 
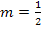und dem y-Achsenabschnitt 
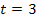. Sie verläuft daher zwischen 
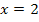und 
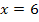oberhalb der x-Achse. Betrachte dazu die folgende Abbildung!
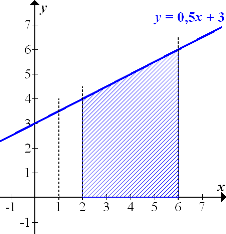
Das Integral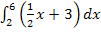 
entspricht der Fläche zwischen 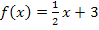und der x-Achse von 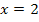bis 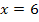. Die entsprechende Fläche ist in der obigen Abbildung blau schraffiert.
Das Integral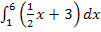 
entspricht der Fläche zwischen 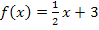und der x-Achse von 
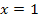bis 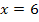. Die entsprechende Fläche ist in der nächsten Abbildung rosa schraffiert.
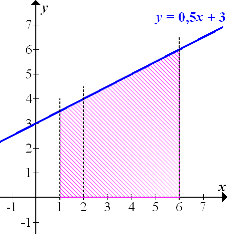
Die Fläche von 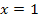bis 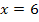ist natürlich größer als die Fläche von 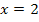bis 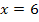. Daher muss auch das Integral 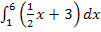größer sein als Integral 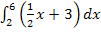. Wenn man nun von der kleineren Fläche 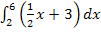die größere 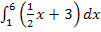abzieht, muss logischerweise ein negatives Ergebnis herauskommen. Daher liefert der Term 
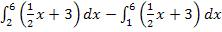zwangsläufig etwas Negatives. So erklärt sich das negative Vorzeichen des Ergebnisses -3,75. Aus unserem Ergebnis
folgt auch, dass die rosa schraffierte Fläche 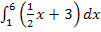um 3,75 FE (Flächeneinheiten) größer ist als die blau bzw. lila schraffierte Fläche .
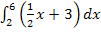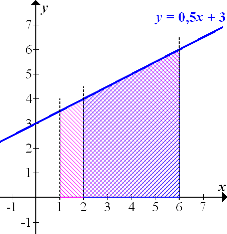
Anmerkung:Die Fläche zu 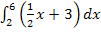erscheint in dieser Abbildung eher lila;das kommt durch die Überlagerung der rosafarbenen Schraffierung von 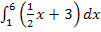mit der blauen Schraffierung .
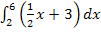Das negative Ergebnis des Integrals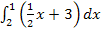 
lässt sich auch folgendermaßen erklären:Die ausschließlich rosa schraffierte Fläche zwischen 
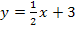und der x-Achse von x = 1 bis x = 2 liegt oberhalb der x-Achse. Da wir aber von der größeren Grenze 2 zur kleineren Grenze 1 integrieren (also in die „falsche Richtung“), ist das Integral 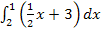negativ. Würden wir die Grenzen vertauschen, würden wir ein positives Ergebnis erhalten:
Die in der obigen Abbildung ausschließlich rosa schraffierte Fläche hat einen Inhalt von 3,75 FE.
Mit der Formel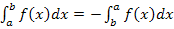 
ergibt sich:
Zu 4c.)
Hier noch einmal die Angabe: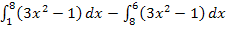 
Vorsicht:Es sieht im ersten Moment vielleicht für dich so aus, als wenn sich die beiden Integrale wieder zu einem einzigen Integral zusammenfassen ließen, weil die obere Grenze des ersten Integrals genau mit der unteren Grenze des anderen Integrals zusammenfällt. Leider steht aber vor dem zweiten Integral ein Minus. Zwei Integrale der gleichen Funktion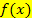 
lassen sich aber nur dann zusammenfassen, wenn die Grenzen zusammenstoßen und wenn die Integrale addiert werden. Um das Minus zu beseitigen, könnte man zwar die Grenzen des zweiten Integrals vertauschen, doch stimmt dann die obere Grenze des ersten Integrals nicht mehr mit der unteren des zweiten überein. Die Integrale stoßen dann also nicht mehr direkt aneinander. Entweder stimmen hier die Vorzeichen der Integrale oder es passen die Grenzen, aber eben nicht beides zusammen!
