Das bestimmte und das unbestimmte Integral
Zu 2b.)
Hier noch einmal die Angabe: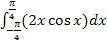 
Die Grenzen sind wieder symmetrisch. Also untersuchen wir die Symmetrie der Integrandenfunktion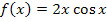 
. Die Funktion ist ein Produkt aus der punktsymmetrischen Teilfunktion 
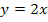(ungerade Potenz) und der achsensymmetrischen Teilfunktion 
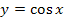. Wir haben oben schon besprochen, dass gilt:
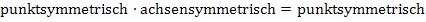
Daher muss die Integrandenfunktion 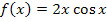punktsymmetrisch zum Ursprung sein.
Rechnerischer Nachweis der Punktsymmetrie (zum Ursprung):
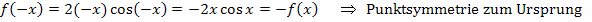
Wir können also wieder den folgenden Zusammenhang ausnutzen:
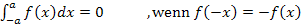
Somit muss das Integral gleich Null sein: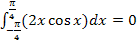 
Auf andere Art und Weise kannst du dieses Integral nicht berechnen, denn du kannst keine Stammfunktion zu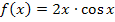 
finden. Vorsicht: 
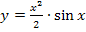ist keine Stammfunktion zu 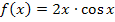! Du darfst keinesfalls die Faktoren 
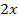und 
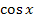einzeln integrieren.
Zu 2c.)
Hier noch einmal das zu berechnende Integral: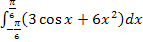 
Die Grenzen sind symmetrisch;die Integrandenfunktion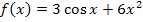 
ist eine Summe aus zur y-Achse symmetrischen Funktionen. Die Summe zweier achsensymmetrischer Funktionen ist wieder achsensymmetrisch. Daher ist 
eine achsensymmetrische Funktion.
Rechnerischer Nachweis der Symmetrie:
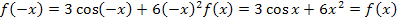
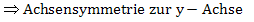
Wir können daher den folgenden Zusammenhang nutzen:
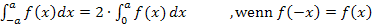
Das gesuchte Integral 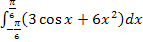muss auf Grund der Achsensymmetrie von doppelt so großsein wie das Integral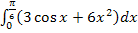 
. Dies nutzen wir bei der Berechnung des Integrals aus.
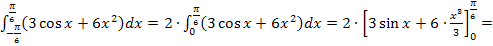
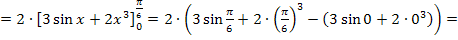
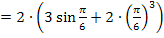
Mit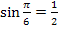 
ergibt sich:
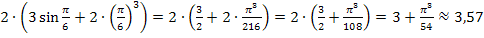
Zu 2d.)
Hier noch einmal das Integral, dessen Wert zu ermitteln ist: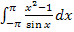 
Du erkennst es bestimmt selbst:Die Funktion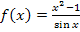 
ist ein Quotient aus einer achsensymmetrischen Funktion (nur gerade Potenzen von x) und einer punktsymmetrischen Funktion. (Die Sinus-Funktion ist, wie gesagt, punktsymmetrisch zum Ursprung.) Die gesamte Funktion ist daher punktsymmetrisch zum Ursprung.
Rechnerischer Nachweis der Symmetrie:
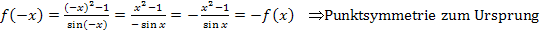
Da auch die Integrationsgrenzen symmetrisch sind, gilt:
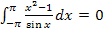
Hinweis:Eine Stammfunktion zu 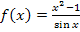brauchst du nicht ermitteln zu können;das ist viel zu schwer.
Vorsicht: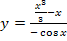 
ist keine Stammfunktion zu 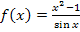. Niemals Zähler und Nenner eines Bruchs einzeln integrieren!
Damit ist diese Aufgabe gelöst!
Im Folgenden werden wir uns noch mit einigen weiteren Eigenschaften des bestimmten Integrals beschäftigen.
Bisher haben wir nur Integrale berechnet, bei denen von links nach rechts, also von der kleineren Zahl zur größeren Zahl integriert wurde. Die untere Grenze war immer die kleinere Zahl und die obere war immer die größere Zahl. Das muss jedoch nicht immer der Fall sein. Die Grenzen können praktisch vertauscht sein, wie beim ersten der beiden Integrale im folgenden Beispiel.
3. Bsp.:
Berechne die folgenden beiden Integrale und vergleiche ihre Ergebnisse!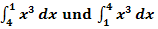 
Lösung:
Beim ersten der beiden Integrale ist die obere Grenze niedriger als die untere. Dennoch musst du dich beim Ausrechnen des Integrals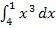 
an die Regel „obere Grenze minus untere“ halten.
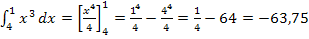
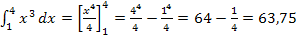
Wenn du die Ergebnisse der beiden Integrale vergleichst, stellst du natürlich sofort fest, dass sie sich nur in ihrem Vorzeichen unterscheiden. Das Vertauschen der Grenzen führt also dazu, dass sich das Vorzeichen des Integrals umdreht. Dies ist nicht nur in diesem Beispiel der Fall, sondern generell.
Merke:Vertauscht man die Grenzen eines bestimmten Integrals, so dreht sich das Vorzeichen des Integrals um!
Es gilt:
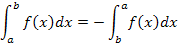
Daraus folgt:Integriert man in die „falsche“ Richtung, also von der größeren zur kleineren Zahl, ist das Integral negativ, wenn die Fläche oberhalb der x-Achse liegt oder die Flächenbilanz an sich positiv wäre. Umgekehrt ist das Integral positiv, wenn man in die „falsche“ Richtung integriert und die Fläche unterhalb der x-Achse liegt oder die Flächenbilanz an sich negativ wäre.
Dies werden wir nun auch beweisen. Aber keine Angst;der Beweis ist nicht schwierig!
Beweis der Formel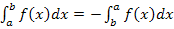 
:
Linke Seite: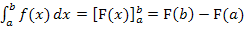 
Rechte Seite: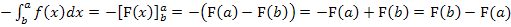 
Linke und rechte Seite liefern beide dasselbe Ergebnis. Damit ist die Formel bewiesen.
Eine andere wichtige Eigenschaft des bestimmten Integrals ist die sogenannte Intervalladditivität oder kurz Additivität. Damit ist gemeint, dass man mehrere Integrale derselben Integrandenfunktion zu einem einzigen Integral zusammenfassen darf, wenn ein Pluszeichen zwischen den Integralen steht und die Grenzen der einzelnen Integrale genau zusammenstoßen. Die obere Integrationsgrenze des ersten Integrals muss also mit der unteren Grenze des zweiten Integrals übereinstimmen. Als mathematische Formel geschrieben:
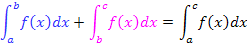
Anschaulich kannst du dir diesen Zusammenhang mit Hilfe der nachfolgenden Abbildung vorstellen.
