Das bestimmte und das unbestimmte Integral

Das Einsetzen der Grenzen ist nicht mehr problematisch. Setzte aber vorsichtshalber immer eine runde Klammer um den Ausdruck, der sich durch das Einsetzen der unteren Grenze ergibt. Dieser Ausdruck soll schließlich komplett abgezogen werden. Ohne Klammer passieren an dieser Stelle erfahrungsgemäßoft Vorzeichenfehler.

Zu 1b.)

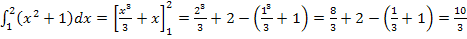
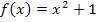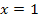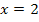Der Flächeninhalt der Fläche, die zwischen der Funktion , der x-Achse sowie den senkrechten Geraden und liegt, beträgt 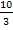FE (Flächeneinheiten). Das Integral entspricht hier genau der Fläche A zwischen Funktion und x-Achse, da die Funktion 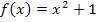oberhalb der x-Achse verläuft. Die Funktion 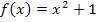ist schließlich eine um 1 nach oben verschobene Normalparabel. Mehr zu Parabeln im Kapitel:Quadratische Funktionen (Parabeln)

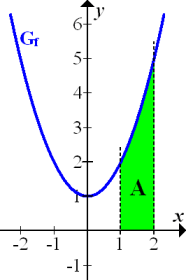
Abb.:Graph 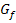der Funktion 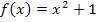mit der Fläche A, die durch das bestimmte Integral 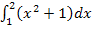berechnet wird.

Hast du inzwischen überlegt, warum man bei bestimmten Integralen die additive Konstante C weglassen darf? Wenn du den Grund noch nicht herausgefunden hast, solltest du die Berechnung des Integrals dieser Teilaufgabe jetzt noch einmal aber mit „+ C “ durchführen.

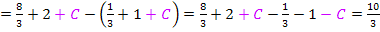
Wie du sehen kannst, hebt sich bei einem bestimmten Integral C am Schluss sowieso weg. Daher kann C bei bestimmten Integralen grundsätzlich von Anfang an weggelassen werden.

Achtung:Dass man C weglassen darf, gilt wirklich nur für bestimmte Integrale, d.h. Integrale mit Integrationsgrenzen. Bald werden wir auch sogenannte unbestimmte Integrale besprechen. Unbestimmte Integrale haben keine Grenzen und bei der Berechnung solcher Integrale darf C keinesfalls weggelassen werden! Es soll an dieser Stelle nur kurz erwähnt werden, dass das unbestimmte Integral 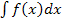im Prinzip nur eine andere Schreibweise für die Menge aller Stammfunktionen 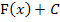ist. Mehr dazu folgt etwas weiter unten in diesem Teil.

Anmerkung:Diese Aufgabe kann auch mittels der sogenannten Streifenmethode gelöst werden. Mit dieser allerdings sehr aufwendigen Methode lassen sich die Formeln zur Berechnung bestimmter Integrale herleiten. Die Herleitung einiger Grundintegrale findest du im gesonderten Teil:Das Summenzeichen und die Streifenmethode

Zu 1c.)

Es soll das Integral 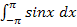berechnet und anschaulich gedeutet werden. Zuerst berechnen wir es, dann wollen wir sehen, was das Ergebnis aussagt.

Um das bestimmte Integral 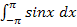zu berechnen, benötigt man erst mal eine Stammfunktion 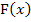zu .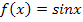

Du weißt bestimmt, dass 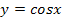abgeleitet 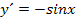ergibt. Daher ist 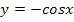abgeleitet 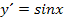. Entsprechend ist eine Stammfunktion zu .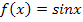

Jetzt kannst du das gesuchte Integral sicher berechnen. Los geht´s!

Zu deiner Kontrolle hier der Lösungsweg:

Die letzten Schritte kannst du mit dem Taschenrechner ausrechnen oder dir im Kopf überlegen. (Wenn du den Taschenrechner verwendest, keinesfalls vergessen, den Mode RAD vorweg einzustellen. 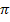ist schließlich ein Winkel im Bogenmaß!)

Hinweis: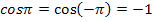

Das Integral 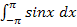ist also gleich Null. Was bedeutet dies nun? Um das zu verstehen, solltest du dir den Graph der Funktion 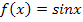in ein Koordinatensystem zeichnen. Außerdem trägst du auch die Grenzen des Integrals, also die senkrechten Geraden 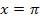und ein und markierst die Fläche zwischen dem Graph und der x-Achse von 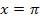bis . Deine Zeichnung muss vom Prinzip her aussehen wie die folgende Abbildung.

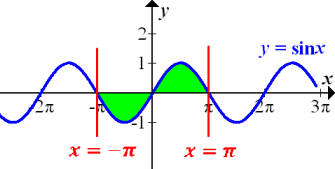
Abb.:Zum Integral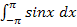

Graph der Funktion 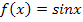mit der Fläche von bis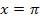

Nun denken wir uns das Integral 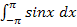bei x = 0 aufgeteilt.

In dieser Abbildung sind zwei Flächenstücke farbig markiert. Die rosafarbene Fläche entspricht dem Integral . Die hellblaue Fläche entspricht dem Integral . Die beiden Flächenstücke sind auf Grund der Punktsymmetrie der Sinus-Funktion gleich groß. (Die Funktion 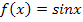ist bekanntlich punktsymmetrisch zum Ursprung, was auch in der Abbildung gut zu erkennen ist.) Die rosafarbene Fläche liegt unterhalb der x-Achse;daher wird dieser Flächenanteil negativ gezählt. Das Integral ist deshalb negativ. (Rechne das gleich mal alleine nach!) Das Integral ist vom Betrag her gleichgroß, aber das Vorzeichen ist positiv, weil die hellblaue Fläche oberhalb der x-Achse liegt. Die beiden Integrale heben sich insgesamt gegenseitig auf. Man sagt:Die Flächenbilanz ist gleich Null. Daher gilt für das gesuchte Integral: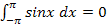

Damit ist die Aufgabe gelöst.

Wir können aus den Erkenntnissen, die wir in Teilaufgabe 1c.) gewonnen haben, eine allgemeine Regel herleiten. Ist eine Funktion 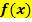punktsymmetrisch zum Ursprung und liegen die Integrationsgrenzen ebenfalls symmetrisch zum Koordinatensystem bei 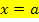und 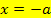, hat das zugehörige Integral immer den Wert Null.

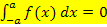
Man kann sich dann jede weitere Rechnung sparen und direkt das Ergebnis 0 hinschreiben. Die Flächenstücke oberhalb und unterhalb der x-Achse sind wegen der Punktsymmetrie zum Ursprung von f zwangsläufig gleich groß. Sie heben sich praktisch gegenseitig auf. Die Flächenbilanz ist gleich Null und somit auch das Integral. Vergleiche dazu die folgende Abbildung!

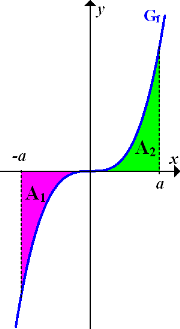
Abb.:Graph einer zum Ursprung punktsymmetrischen Funktion, es gilt

Das Integral 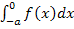entspricht in der Abbildung der lilafarbenen Fläche 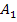. Die Fläche 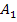liegt unterhalb der x-Achse und wird daher bei der Flächenbilanz negativ gewertet. Das Integral 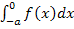ist hier deshalb negativ.

Das Integral entspricht in der Abbildung der grünen Fläche 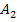. Die Fläche 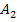liegt oberhalb der x-Achse und wird daher bei der Flächenbilanz positiv gewertet. Das Integral hat hier deshalb einen positiven Wert.

Der Inhalt der beiden Flächenstücke 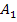und 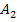ist jeweils gleich großauf Grund der symmetrischen Lage der Grenzen a und – a sowie der Punktsymmetrie zum Ursprung des Graphen von .

Die beiden Integrale 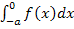und sind deswegen vom Betrage her gleich groß;sie haben aber unterschiedliche Vorzeichen. Sie heben sich daher insgesamt in der Flächenbilanz gegenseitig auf;die Flächenbilanz von – a bis a ist Null.

Es gilt allgemein für Funktionen , die punktsymmetrisch zum Ursprung sind:

Die Punktsymmetrie zum Ursprung von muss aber rechnerisch nachgewiesen werden mit . Siehe auch:Symmetrieverhalten:Achsen – und Punktsymmetrie zum Koordinatensystem

Das Ganze noch einmal, nur mathematisch geschrieben:

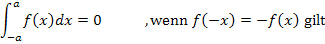
Damit kannst du das Ergebnis eines bestimmten Integrals einer zum Ursprung punktsymmetrischen Funktion angeben, obwohl du eventuell gar keine Stammfunktion F(x) zu ermitteln kannst. Das funktioniert aber wirklich nur dann, wenn sich die obere und die untere Grenze bloßim Vorzeichen unterscheiden und punktsymmetrisch zum Ursprung ist.

Ist eine Funktion 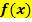dagegen achsensymmetrisch zur y-Achse, d.h. es ist 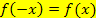erfüllt, dann ist das gesamte Integral doppelt so groß wie das Integral 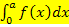oder wie das Integral 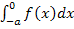. Die beiden Integrale 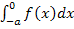und sind auf Grund der Symmetrie der Grenzen und wegen der Achsensymmetrie der Funktion gleich groß;nicht nur vom Betrag, sondern auch vom Vorzeichen her.

Das Integral 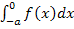entspricht in der folgenden Abbildung der lilafarbenen Fläche 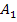. Das Integral entspricht in der folgenden Abbildung der grünen Fläche 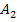. Beide Flächenstücke sind auf Grund der symmetrischen Lage der Grenzen a und – a sowie des achsensymmetrischen Graphen von absolut gleich groß. Daher lassen sich Integrale mit symmetrischen Grenzen bei achsensymmetrischen Funktionen geschickt berechnen mit der folgenden Formel:

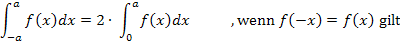
Abb.:Graph 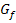einer zur y-Achse achsensymmetrischen Funktion mit den gleich großen Flächenstücken 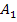und 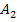, daher gilt:

Die Achsensymmetrie zur y-Achse von muss aber rechnerisch nachgewiesen werden mit . Siehe auch:Symmetrieverhalten:Achsen – und Punktsymmetrie zum Koordinatensystem

Integrale mit der unteren Grenze 0 lassen sich meist schneller und einfacher berechnen, als andere Integrale.

---