Das bestimmte und das unbestimmte Integral
Hast du die Ergebnisse herausgefunden?
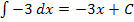
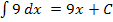
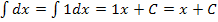
Beim Integrieren einer Konstanten (d.h. einer festen Zahl ohne Variable) nach dx kommt einfach ein x dazu.
Entsprechend funktioniert nun auch das Integrieren nach dt. Bei der Integration einer Konstante nach dt kommt einfach ein t dazu.
Überlege dir doch kurz, was die Integrale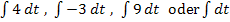 
ergeben würden!
Du bist sicher selbst auf folgende Ergebnisse gekommen:
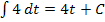
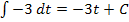
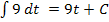
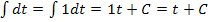
Nun aber wieder zurück zu unserer Aufgabe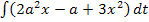 
. Es soll nach dt integriert werden;t ist hier die Variable. Alle anderen Buchstaben müssen als Parameter betrachtet werden, also als konkrete Zahlen. Bei keinem der Faktoren der Integrandenfunktion kommt die Variable t vor. Daher müssen alle drei Faktoren als Konstanten betrachtet werden. Wie man eine Konstante nach dt integriert, haben wir oben gerade geübt. Jetzt müsstest du die Aufgabe eigentlich alleine lösen können. Na, was kommt wohl heraus?
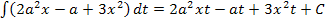
Dieses Beispiel war wirklich nicht einfach. Du solltest daran jedoch lernen, dass es sehr wichtig ist, ob hinter dem Integral dx, dt oder etwa da steht. Nur daran kannst du erkennen, welcher Buchstabe die Variable ist, also derjenige Buchstabe nach dem integriert werden soll. Die Integrale aus 11b.) und 11c.) stellen natürlich sehr seltene Sonderfälle dar. Meistens wirst du nur mit Integralen zu tun haben, die genau einen Buchstaben in der Integrandenfunktion enthalten und nach eben diesem Buchstaben sollst du dann auch integrieren. Ob du nun beispielsweise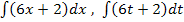 
oder 
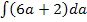ausrechnen sollst, läuft ja praktisch auf das gleiche hinaus.
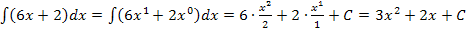
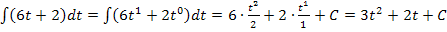
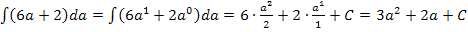
Gelegentlich kann es auch vorkommen, dass du beim Aufstellen der Gleichung von Polynomfunktionen Integrale der folgenden Form oder ähnliche lösen musst:
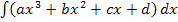
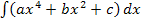
Versuch´s doch gleich alleine, ohne auf die folgende Lösung zu schauen!
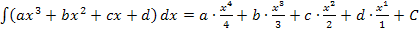
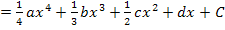
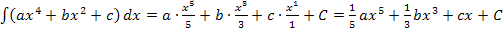
Brauchen kann man das vor allem bei Aufgaben des folgenden Typs:
Gesucht ist die Gleichung einer Polynomfunktion (unbekannten Grades), deren zweite Ableitung und zwei weitere Informationen angegeben sind, z.B. ein Kurvenpunkt und die zugehörige Tangentensteigung oder zwei Kurvenpunkte. Schauen wir uns zum Abschluss dieses Teils ein Beispiel für so eine Aufgabe an.
12. Bsp.:Gleichung einer Polynomfunktion gesucht
Die zweite Ableitung einer Polynomfunktion lautet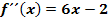 
. Außerdem ist bekannt, dass die Funktion das Extremum 
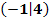besitzt. Welche Gleichung hat die Funktion?
Lösung:
Um von der zweiten Ableitung auf die Funktion 
zu kommen, muss zweimal integriert werden.
