Das bestimmte und das unbestimmte Integral
Dann musst du 1 zum Exponenten von x dazuzählen und außerdem durch den neuen Exponenten teilen.
Vorüberlegung mit a = 7:
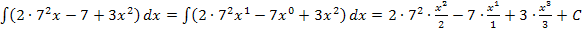
Wir rechnen das Ergebnis nur soweit aus, wie das auch möglich gewesen wäre, wenn man für a nicht die Zahl 7 eingesetzt hätte. So ergibt sich:
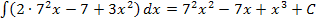
(Diese Vorüberlegung gehört nicht wirklich zur Lösung der Aufgabe. Du solltest sie entweder im Kopf durchführen oder auf einem Schmierblatt. Dein Lehrer braucht das nicht zu sehen. Besser ist es natürlich, wenn du die Aufgabe auch ohne Vorüberlegung direkt lösen kannst.)
Wie in der Aufgabe verlangt, machen wir nun das Gleiche, nur dass wir für a nichts Konkretes einsetzen.
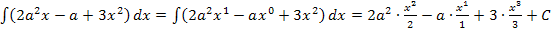
Den ersten Zwischenschritt mit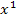 
und 
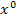kannst du natürlich weglassen und sofort das Ergebnis hinschreiben. Nachdem man nun noch gekürzt hat, erhält man das Endergebnis:
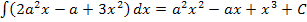
Zu 11b.)
Es ist das Integral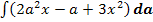 
zu berechnen. Wir müssen also nach da integrieren. Dabei sind nur die Potenzen von a wichtig. Nur bei diesen Potenzen wird der Exponent um 1 erhöht und außerdem durch den um 1 erhöhten Exponenten geteilt. x musst du jetzt wie eine feste Zahl behandeln;x ist nun eine Konstante, so wie in Teilaufgabe 11a.) der Buchstabe a. Versuche es doch gleich ´mal alleine!
Du solltest auf folgendes Ergebnis gekommen sein:
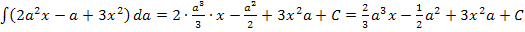
Zu schnell? Ok, dann noch einmal ganz langsam. Konzentriere dich nur auf die Potenzen von a. Bei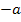 
denken wir uns den Exponenten 1 dazu, und weil bei 
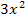kein a dabeisteht, denken wir uns 
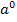dazu.
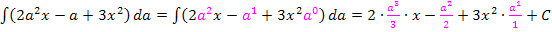
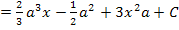
Zu 11c.)
Hier noch einmal die Angabe: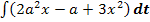 
Das ist kein Tippfehler! Hier steht wirklich „ dt “ hinter dem Integral, obwohl gar kein t bei der Integrandenfunktion vorkommt. Wenn dir das eigenartig vorkommt, dann denk doch ´mal an Integrale der Form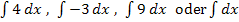 
. Bei diesen Integralen soll nach dx integriert werden;es kommt aber kein x im Integranden vor. Wie würdest du denn diese Integrale lösen? Vergiss nicht, dass das Integrieren quasi das Gegenteil des Ableitens ist. Willst du beispielsweise das Integral 
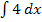berechnen, musst du dich fragen, welche Funktion F(x) abgeleitet die Integrandenfunktion 
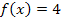ergibt. Bist du selbst auf die Lösung gekommen? Die Funktion F(x) = 4x ergibt abgeleitet genau 4. Man kann sich das auch wieder mit der Integrationsregel 
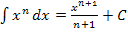herleiten. Um diese Regel anwenden zu können, schreibt man 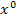hinter die Zahl 4.
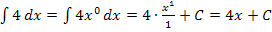
Nun kannst du bestimmt auch die Integrale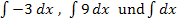 
berechnen. (Denk dir bei dem letzten Integral die Zahl 1 dazu.) Bitte erst einmal selbst nachdenken, bevor du weiterliest!
