Das bestimmte und das unbestimmte Integral

11. Bsp.:

Berechne folgende unbestimmte Integrale!

a.)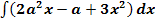

b.)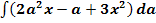

c.)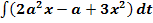

Lösung:

In dieser Aufgabe soll die gleiche Funktionenschar einmal nach dx, einmal nach da und ein weiteres Mal nach dt integriert werden. Das bedeutet, dass du dich beim Integrieren einmal nur auf die Potenzen von x, einmal nur auf die Potenzen von a und einmal nur auf die Potenzen von t konzentrieren musst. Soll beispielsweise (vgl. Teilaufgabe 10b.) nach da integriert werden, geht es nur um die Potenzen von a;alle anderen Buchstaben musst du dir als konkrete Zahlen denken. Steht also hinter dem Integral „da“, wie in Teilaufgabe 10b.), ändern sich nur die Potenzen von a. Bloßbei diesen Potenzen wird zum Exponenten 1 dazugezählt und außerdem durch den neuen Exponenten geteilt. Andere Buchstaben müssen als Konstanten (feste Zahlen) angesehen werden.

Vorsicht:Beim Integrieren nach da oder dt stellt x eine konstante Zahl und nicht mehr die Variable dar, nach der man integriert.

Beim Integrieren nach da ist schließlich a die Variable, nach der logischerweise integriert wird. Beim Integrieren nach dt ist entsprechend t die Variable.

Nur auf die Potenzen der Variablen schauen, wenn du integrierst! (Die Variable ist immer der Buchstabe, der beim Integral ganz am Ende hinter dem d steht.)

Zu 11a.)

In dieser Teilaufgabe soll das Integral 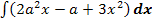berechnet, d.h. nach dx integriert werden. Das erkennt man logischerweise daran, dass hinter dem Integral dx steht und nicht etwa da oder dt. Bloß, was bedeutet es genau, wenn man nach dx integrieren soll? Im Prinzip ganz einfach:Die Variable ist der Buchstabe x , so wie du das gewohnt bist. Beim Integrieren musst du dich nur auf die Potenzen von x konzentrieren;alle anderen Buchstaben sind nur sogenannte Parameter, also irgendwelche Konstanten. Eine Konstante ist eine feste Zahl, die man bloßnicht kennt. Der Ausdruck 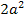ist praktisch als Zahl zu betrachten, ebenso .

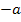Wenn du Probleme hast dir diese Ausdrücke als Zahlen vorzustellen, setzt du vorweg – am besten in Gedanken – irgendeine konkrete Zahl für a ein, zum Beispiel 7. (Die Zahl 7 wurde rein willkürlich gewählt.) Dann überlegst du dir, wie du dieses Integral lösen würdest.

Denk daran, dass x eigentlich 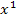ist und, dass man bei einer Konstante (Zahl ganz ohne x) auch 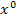dazuschreiben schreiben könnte;es gilt nämlich 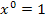und die Multiplikation mit 1 verändert nichts. (Z. B.: 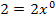oder 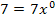und somit auch 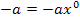) Dadurch müsstest du leichter integrieren können.

---