Das bestimmte und das unbestimmte Integral
Jetzt müsstest du es alleine schaffen, das Integral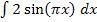 
zu berechnen. Versuch´s erst alleine, bevor du dir die Lösung anschaust!
Hast du es dir wirklich selbst überlegt?
Ok, dann jetzt endlich die Lösung:
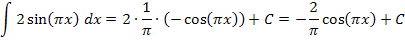
Zu 10d.)
Gesucht ist das Ergebnis von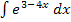 
. Du weißt sicher, dass 
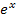abgeleitet 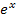ergibt. Umgekehrt ist 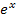integriert auch wieder 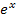. Es gilt: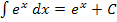 
Was ergibt dann deiner Meinung nach ?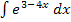
Wenn du denkst, dass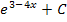 
das Ergebnis ist, liegst du leider nicht ganz richtig, aber auch nicht ganz falsch – es fehlt nur etwas. Bloßwas?
Jetzt bitte erst einmal selbst nachdenken!
Denke daran, dass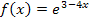 
eine verkettete Funktion ist mit 
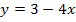als innerer Funktion. Überlege dir, mit was du beim Ableiten nachdifferenzieren müsstest. Durch diese Zahl musst du dann beim Integrieren teilen bzw. mit dem Kehrwert multiplizieren.
Du bist hoffentlich inzwischen d´rauf gekommen:
Es fehlte der Faktor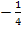 
.
Die Lösung ist nämlich: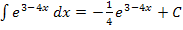 
Es handelt sich bei den Integralen der letzten drei Teilaufgaben um Integrale sogenannter linear transformierter Funktionen. Eine lineartransformierte Funktion ist eine Funktion, in die für x eine lineare Funktion, also ein Ausdruck der Form m x + t, eingesetzt ist. Als Grundfunktion bezeichnet man dabei die Funktion 
, in die der Ausdruck m x + t eingesetzt ist.
Bei der Funktion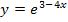 
ist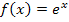 
die Grundfunktion. Wenn du die Reihenfolge der Faktoren im Exponenten bei 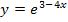umdrehst, erhältst du 
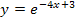. Daran erkennst du, dass im Exponenten die lineare Funktion 
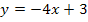steht, also ein Ausdruck der Form m x + t. Dieser Ausdruck ist in die Grundfunktion 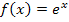für x eingesetzt. Man kann somit die Funktion 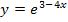als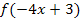 
schreiben.
Linear transformierte Funktion in allgemeiner Form: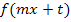 
Bei der Integration solcher Funktionen musst du zuerst eine Stammfunktion der Grundfunktion ermitteln, wobei du statt x den Ausdruck m x + t schreiben und außerdem noch mit 
multiplizieren musst.
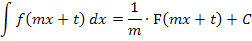
Wenn dir das noch nicht so hundertprozentig einleuchtet, gehe zu Weitere Integrationsregeln. Dort findest du noch mehr Aufgaben dieses Typs und noch ausführlichere Erklärungen. Wie du auch bei anderen schwierigeren Funktionen eine Stammfunktion finden kannst, wird ebenfalls erklärt im Teil Weitere Integrationsregeln.
Bisher haben wir fast immer nach x integriert. Hinter dem Integral stand in der Regel dx. Zum Abschluss dieses Teils wollen wir uns noch mit Integralen beschäftigen, bei denen nach einer anderen Variablen integriert werden muss. Schwierig wird es vor allem, wenn mehrere verschiedene Buchstaben im Integranden auftreten.
