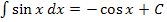Das bestimmte und das unbestimmte Integral
Du weißt, dass man durch einen Bruch dividiert, indem man mit dem Kehrwert multipliziert. Die Brüche in den Exponenten sollen auch nicht einfach stehen gelassen werden. Um sie umzuformen, verwenden wir das folgende Potenzgesetz: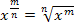 
So ergibt sich: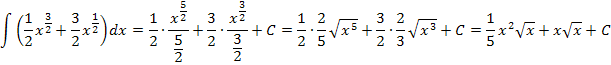 
Im letzten Schritt wurde teilweise radiziert, d.h. teilweise die Wurzel gezogen. Dir ist dieser Schritt nicht klar? Ok, dann noch einmal langsam mit Zwischenschritten:
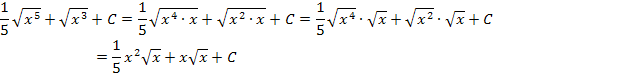
Zu 10b.)
Es soll das unbestimmte Integral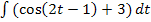 
berechnet werden. Statt der sonst üblichen Variablen x kommt hier die Variable t vor. Das ist aber kein Problem;es soll schließlich auch nach dt integriert werden. Du denkst dir einfach statt t ein x. Das Problem ist hier vielmehr, dass 
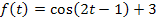eine verkettete Funktion ist. Wie man verkettete Funktionen ableitet, weißt du hoffentlich:Äußere Funktion ableiten, dabei statt x bzw. hier t die innere Funktion hinschreiben und die innere Funktion nachdifferenzieren, d.h. mit der Ableitung der Inneren multiplizieren. Beim Integrieren müssen wir entsprechend umgekehrt vorgehen. Die äußere Funktion, also hier der Kosinus, muss integriert werden, die innere Funktion, also 
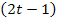bleibt dabei stehen. Wollte man 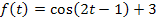ableiten, müsste mit der Ableitung der inneren Funktion 
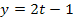, d.h. mit der Zahl 2, multiplizieren. Beim Integrieren von 
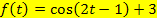muss daher entsprechend durch die Zahl 2 dividiert werden oder mit 
multipliziert werden. Das darfst du auf keinen Fall vergessen.
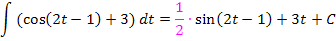
Wenn dir das mit dem Faktor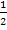 
beim Integrieren nicht so ganz klar ist, solltest du versuchen die Funktion 
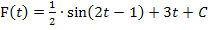mit Hilfe der Kettenregel abzuleiten. Dabei musst du mit dem Faktor 2 nachdifferenzieren. Diese 2 hebt sich dann mit der Zahl 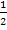wieder auf und es kommt, wie bei einer Stammfunktion verlangt, 
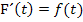heraus.
Zu 10c.)
Es soll das Integral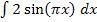 
berechnet werden. Dabei tritt das gleiche Problem auf, das bereits in Teilaufgabe 8b.) erläutert wurde. 
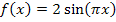ist eine verkettete Funktion. Dabei ist 
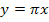die innere Funktion. Lass dich nicht durch 
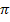erschrecken. 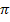ist schließlich auch nur eine Zahl, nämlich ungefähr 3,14. Wolltest du die Funktion 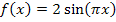ableiten, müsstest du laut Kettenregel mit 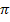nachdifferenzieren. 
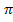ist ja die Ableitung der inneren Funktion 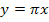. Bei der Integration von 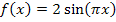muss umgekehrt durch 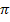geteilt werden bzw. mit 
multipliziert werden. Die Zahl 2, die vor dem Sinus steht, ist eine multiplikative Konstante, sie wird beim Integrieren einfach abgeschrieben. Außerdem musst du noch bedenken:Sinus ergibt integriert minus Kosinus: 
