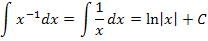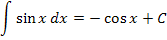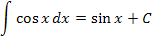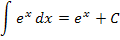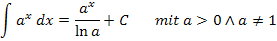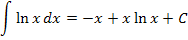Das bestimmte und das unbestimmte Integral

Summen und Differenzen dürfen einzeln integriert werden, Produkte und Quotienten dagegen nicht. Das ist auch ausführlich erklärt im Teil Die Stammfunktion F(x) und einfache Integrationsregeln.

Beispiel: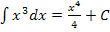

Damit ist gemeint, dass 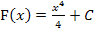Stammfunktion zur Funktion 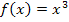ist, was gleichbedeutend ist mit .

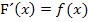Wichtig:Bei unbestimmten Integralen darfst du keinesfalls die additive Konstante, also das „+ C “ vergessen!

Eigentlich stellt das unbestimmte Integral nur eine andere Schreibweise für die Menge aller Stammfunktionen 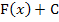einer Funktion dar.

Hier eine Übersicht der wichtigsten Grundintegrale:

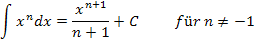
Eine multiplikative Konstante a darf vor das Integral gezogen werden. Es gilt nämlich:

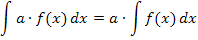
Beispiel: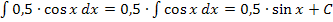

Eine multiplikative Konstante ist eine konkrete Zahl ohne x, welche mit irgendetwas multipliziert wird oder durch die dividiert wird. Solche Zahlen werden beim Integrieren einfach abgeschrieben;nur die restliche Funktion wird integriert.

Summen und Differenzen zweier Funktionen und 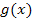dürfen einzeln, also Funktion für Funktion, integriert werden:

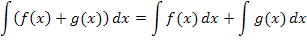
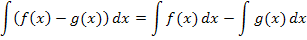
Beispiel: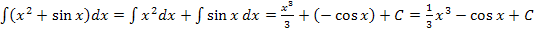

Aber Vorsicht:Produkte und Quotienten zweier Funktionen dürfen dagegen keinesfalls einzeln integriert werden.

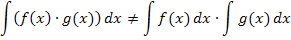
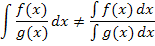
Wenn möglich bei einem Produkt immer zuerst ausmultiplizieren und danach integrieren. Beim Integral eines Quotienten den Bruch falls möglich ausrechnen, indem man jeden Summanden des Zählers einzeln durch den kompletten Nenner teilt. (Dabei kann eine Polynomdivisionnötig sein.) Dann erst integrieren.

Beispiele:

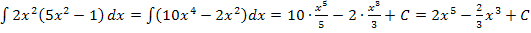
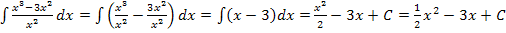
Leider ist es nicht immer so einfach, eine Stammfunktion zu finden. Das kannst du an den nächsten Beispielaufgaben sehen.

10. Bsp.:Berechne die folgenden unbestimmten Integrale!

a.)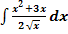

b.)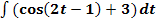

c.)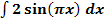

d.)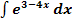

Lösung:

Zu 10a.)

Brüche dürfen bekanntlich nicht einzeln im Zähler und Nenner integriert werden. Wir müssen den Bruch erst umformen, bevor wir integrieren können. Im Zähler steht eine Summe;jeder Summand muss einzeln durch den Nenner dividiert werden. So entstehen zwei Einzelbrüche. Im Nenner kommt jedoch eine Wurzel vor. An Stelle der Wurzel 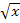schreiben wir im Nenner die Potenz 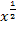. Dann lässt sich das Potenzgesetz 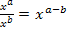anwenden.

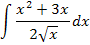
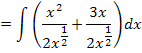
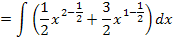
Jetzt kann mit Hilfe der Regel 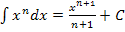integriert werden.

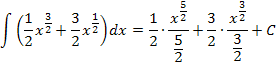
Das Ergebnis muss noch vereinfacht werden.

---