Das bestimmte und das unbestimmte Integral
Deshalb ist es so wichtig, dass du k 
ℤ unbedingt bei der Lösung 
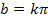dazu schreibst.)
Das gleiche Ergebnis bekommt man natürlich auch durch Rechnung:
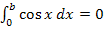
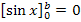
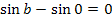
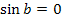
Um die Gleichung 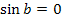zu lösen, stellen wir uns den Graph der Sinus-Funktion vor und überlegen uns, wo ihre Nullstellen liegen.
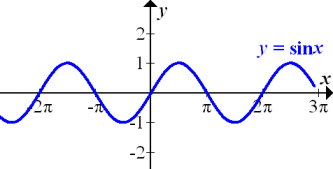
Man erkennt, dass die Sinus-Funktion bei den ganzzahligen Vielfachen von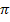 
ihre Nullstellen hat, kurz bei 
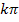mit k ℤ.
Die Gleichung 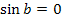wird gelöst durch:
b = 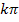mit k ℤ
Dies ist natürlich das gleiche Ergebnis, dass wir oben schon erhielten.
Zu 9b.)
Hier noch einmal die Angabe: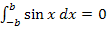 
Diese Aufgabe ist ganz schnell gelöst. Die Integrandenfunktion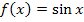 
ist punktsymmetrisch zum Ursprung. Da die Grenzen symmetrisch bei –b und b liegen, ist das Integral für beliebige reelle Werte von b gleich Null. Es ist also völlig egal, was man für b einsetzt;die Gleichung ist immer erfüllt. Deshalb ist die Lösung hier b ℝ.
Damit ist die Aufgabe schon gelöst. Du wärst natürlich zum gleichen Ergebnis gekommen, wenn du die Aufgabe rechnerisch gelöst hättest.
Rechnerische Lösung:
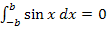
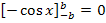
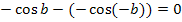
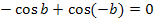
Auf Grund der Achsensymmetrie der Kosinus-Funktion gilt: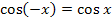 
Damit ergibt sich:
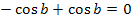
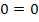
Diese Aussage ist immer wahr, egal für welche Werte von b. Es kommt ja gar kein b mehr vor. Man kann also für b einsetzen, was man will;die Gleichung 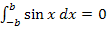ist immer erfüllt. Als Lösung schreibt man:b ℝ
Bisher haben wir uns in diesem Teil ausschließlich mit bestimmten Integralen und ihrer Berechnung beschäftigt. Ein bestimmtes Integral hat immer konkrete Grenzen. Was ist denn nun aber ein unbestimmtes Integral?
Das unbestimmte Integral:
Im Unterschied zum bestimmten Integral hat das unbestimmte Integral keine Grenzen.
Das unbestimmte Integral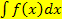 
entspricht der Menge aller Stammfunktionen 
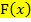einer Funktion 
.
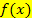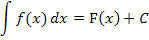
Dabei gilt der Hauptsatz der Differenzial- und Integralrechnung, kurz HDI:
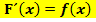
Der HDI besagt somit nichts anderes, als dass das Integrieren quasi das Gegenteil des Differenzierens, also des Ableitens ist.
Mehr zum Thema HDI findest du im Teil Die Integralfunktion und der HDI.
Um ein unbestimmtes Integral zu berechnen, muss man daher genauso vorgehen wie bei der Ermittlung der Stammfunktion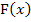 
zu einer Funktion 
. Bei Polynomfunktionen muss man dabei beispielsweise den Exponenten um 1 erhöhen und zusätzlich durch diejenige Zahl teilen, die im neuen Exponenten steht. Allerdings darf man bei unbestimmten Integralen niemals „+ C “ vergessen;bei bestimmten Integralen ist „+ C “ dagegen nicht nötig.
