Das bestimmte und das unbestimmte Integral
Die Flächenbilanz von 0 bis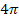 
ergibt Null, weil die Flächenstücke oberhalb der x-Achse positiv in die Flächenbilanz eingehen und die Flächenstücke unterhalb der x-Achse negativ.
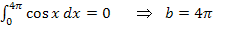
Du hast das Prinzip bestimmt längst erkannt:Bei allen Vielfachen von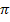 
liegt jeweils eine Lösung, also auch bei 
, 
, 
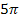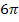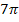usw.
Da laut Angabe b 
ℝ gilt, kann b natürlich auch negativ sein. Wir können somit logischerweise von der y-Achse auch ein Vielfaches von 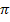nach links gehen, damit die Flächenbilanz gleich Null wird.
So wird die Gleichung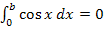 
beispielsweise gelöst durch b = 
.
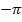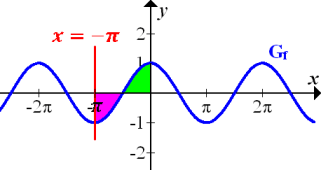
Das grüne Flächenstück ist genauso großwie das rosafarbene Flächenstück. Bei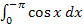 
wird von der größeren zur kleineren Grenze integriert;also in die „falsche Richtung“. Deshalb geht das oberhalb der x-Achse liegende grüne Flächenstück negativ in die Flächenbilanz ein, entsprechend das unterhalb der x-Achse liegende rosa Flächenstück positiv. Das grüne Flächenstück oberhalb und das rosafarbene unterhalb der x-Achse heben sich gegenseitig bei der Flächenbilanz auf. Auch die Flächenbilanz von 0 bis 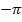ergibt Null.
Somit gilt:
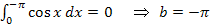
Eine weitere negative Lösung der Gleichung 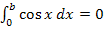lautet:b =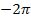 
Anschaulich wird das in der folgenden Zeichnung klar.
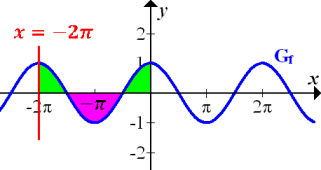
Die beiden grünen Flächenstücke sind gemeinsam genauso großwie das rosafarbene Flächenstück. Die grünen Flächenstücke oberhalb und das rosafarbene unterhalb der x-Achse heben sich gegenseitig bei der Flächenbilanz auf. Somit ergibt auch die Flächenbilanz von 0 bis 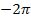Null.
Es gilt:
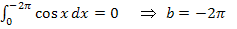
Auf Grund des periodischen Verlaufs der Kosinus-Funktion gilt außerdem:
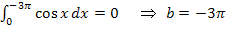
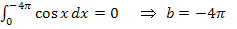
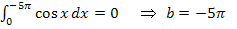
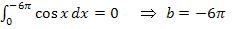
So könnte man jetzt ewig weiter machen und doch können wir auf diese Art und Weise nicht alle Lösungen für b hinschreiben. Da müssen wir uns etwas anderes einfallen lassen. Hast du eine Idee, wie man wirklich alle Lösungen auf einmal hinschreiben kann?
Schau dir noch einmal alle Lösungen an, die wir bereits aufgeschrieben haben:
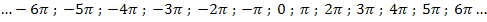
Es handelt sich immer um ganzzahlige Vielfache von 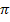. Durch k ist eine beliebige ganze Zahl beschrieben, wenn k ℤ gilt. Daher lassen sich die gesuchten Lösungen folgendermaßen schreiben:
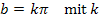
ℤ
Dadurch sind wirklich alle reellen Lösungen beschrieben. (Du erhältst die einzelnen vorher aufgeschriebenen Lösungen, indem du für k jeweils irgendeine ganze Zahl einsetzt. So ergibt sich zum Beispiel mit k = – 3 die Lösung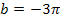 
oder mit k = – 2 die Lösung 
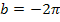. Du darfst für k natürlich nur ganze Zahlen einsetzen.
