Das bestimmte und das unbestimmte Integral
Danach kannst du die angegebene Stammfunktion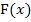 
bei der Berechnung eines bestimmten Integrals 
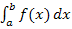einfach in die eckigen Klammern schreiben. Du brauchst dann also nicht selbst zu integrieren!
Achtung:Immer, wenn eine Stammfunktion angegeben ist, musst du sie bei der Berechnung des Integrals auch verwenden, also nicht versuchen selbst zu integrieren. Wenn du selbst eine Stammfunktion finden könntest, warum sollte sie dann angegeben sein!
8. Bsp.:
Zeige: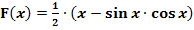 
ist eine Stammfunktion der Funktion 
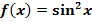. Berechne dann das bestimmte Integral 
!
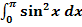Lösung:
Allgemeiner Hinweis: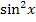 
ist nur eine andere Schreibweise für 
.
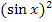Es gilt: 
Wir beginnen mit dem Beweis, dass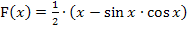 
eine Stammfunktion der Funktion 
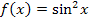bzw. 
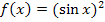ist. Dazu müssen wir nur zeigen, dass 
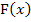abgeleitet genau 
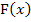ergibt. Du musst also ableiten und dann das Ergebnis so lange umformen, bis herauskommt. Probiere das doch gleich mal selbst!
integrieren, um so auf 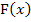zu kommen, können wir hier umgekehrt nicht, weil wir noch keine Integrationsregel für verkettete (verschachtelte) Funktionen kennen. Deshalb ist 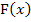ja auch angegeben!
Zu Zeigen: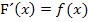 
Du hast Schwierigkeiten dabei? Hier noch ein kleiner Tipp:Verwende beim Vereinfachen der Ableitung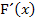 
den sogenannten trigonometrischen Pythagoras! Das ist die folgende Formel:
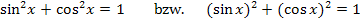
Zu deiner Kontrolle, nun der komplette Rechenweg mit Erläuterungen:
Zum Ableiten von 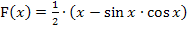muss unter anderem die Produktregel angewendet werden, weil es sich bei dem Ausdruck 
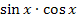um ein Produkt handelt, das in beiden Faktoren die Variable x enthält.
Die Produktregel besagt Folgendes:Ein Produkt zweier Faktoren, welche beide die Variable x enthalten, wird abgeleitet, indem man rechnet:Den ersten Faktor abgeleitet mal den zweiten abgeschrieben plus den ersten Faktor abgeschrieben mal den zweiten Faktor abgeleitet.
Den Faktor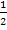 
, der vor der Klammer steht, schreiben wir beim Ableiten einfach ab, da es sich um eine multiplikative Konstante (Zahl ohne x) handelt. (Zahlen ohne x mit Mal oder geteilt bleiben beim Ableiten stehen;Zahlen mit Plus oder Minus fallen dagegen weg.)
Des Weiteren gilt:Sinus abgeleitet ist Kosinus, aber Kosinus ergibt abgeleitet Minus Sinus!
Du musst hier beim Ableiten sehr aufpassen mit den Vorzeichen. Es ist dabei hilfreich sich eine zusätzliche Klammer bei 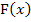zu denken.
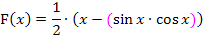
Der Ausdruck innerhalb der rosa Klammer wird nun mit der Produktregel abgeleitet. Durch die Anwendung der Produktregel entsteht bei 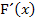innerhalb der rosa Klammer eine Summe. Das Minus vor der rosa Klammer muss sich auf den kompletten Ausdruck innerhalb der rosa Klammer beziehen. Daher ist die rosafarbene Klammer so wichtig.
