Das bestimmte und das unbestimmte Integral
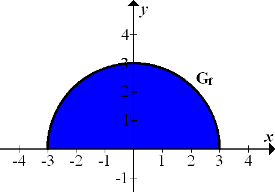
Um den Wert des Integrals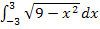 
zu ermitteln, brauchen wir entweder eine Stammfunktion zu 
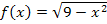oder wir berechnen das Integral elementargeometrisch, d.h. in diesem Fall mit Hilfe der Formel für die Kreisfläche.
Eine Stammfunktion zu 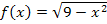können wir nicht finden, da es sich bei 
um eine verkettete Funktion handelt, und wir zum Integrieren (noch) keine Regel für verkettete Funktionen behandelt haben. (Verkettete Funktionen musst du auch im Abitur nur in einigen Sonderfällen integrieren können, aber nicht im Allgemeinen.)
Hinweis:Auf keinen Fall darfst du einfach die Wurzel hinschreiben und nur den Teil integrieren, der unter der Wurzel steht. Das so gewonnene Ergebnis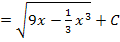 
wäre keine Stammfunktion von . Kontrolliere das ruhig mal selbst. Du weißt:Die Ableitung einer Stammfunktion muss genau die Funktion ergeben.
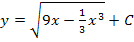ergibt mit der Kettenregel abgeleitet jedoch 
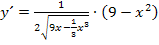und eben nicht .
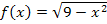Damit ist klar, dass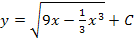 
keine Stammfunktion zu 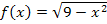ist.
Weil wir keine Stammfunktion zu 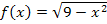finden können, bleibt uns nichts anderes übrig als, dass wir das Integral 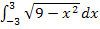elementargeometrisch ausrechnen, d.h. den Flächeninhalt des Halbkreises mit Radius r = 3 ermitteln.
Weißt du die Formel für den Flächeninhalt eines Kreises noch?
Wenn nicht, sie steht auch in der Formelsammlung bzw. auf der Merkhilfe für G8.
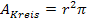
Wir haben hier nur einen Halbkreis vorliegen, daher brauchen wir nur die Hälfte der Kreisfläche, um das Integral 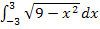zu berechnen.
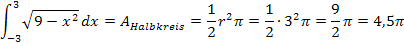
Du siehst, dass wir das Integral zwar nicht auf herkömmlichen Weg mittels Stammfunktion und Einsetzen der Grenzen ausrechnen konnten, aber wenigstens über den Weg mit der Fläche des Halbkreises. Das war natürlich ein besonderer Spezialfall, doch ähnliche Aufgaben finden sich immer wieder in den verschiedensten Schulbüchern.
Merke:
Der Graph einer Funktion der Form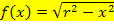 
ist immer ein Halbkreis mit Mittelpunkt M(0|0) und Radius r, der oberhalb der x-Achse, also im I. und II. Quadranten verläuft. Dagegen beschreibt 
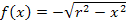einen Halbkreis mit Mittelpunkt M(0|0) und Radius r, der im III. und IV. Quadranten verläuft, d.h. unterhalb der x-Achse.
Oft ist es dir bei komplizierteren Funktionen nicht möglich selbst eine Stammfunktion zu ermitteln. Damit dennoch bestimmte Integrale solcher Funktionen von dir berechnet werden können, wird dann eine Stammfunktion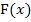 
zu angegeben. Du musst nur noch beweisen, dass 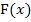wirklich eine Stammfunktion zu ist. Das bedeutet, dass du zeigen musst, dass 
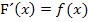gilt.
