Das bestimmte und das unbestimmte Integral
(Obere Grenze eingesetzt minus untere eingesetzt) Das Ganze wird natürlich immer gleich den Wert gesetzt, der beim Integral herauskommen soll. Dadurch ergibt sich letztendlich eine Gleichung, die du nur noch nach a auflösen musst. Versuche das doch gleich mal alleine! Wenn dir noch nicht so ganz klar ist, was du machen sollst, um die Aufgaben zu lösen, schaust du dir einfach den folgenden Rechenweg der Teilaufgabe 6a.) an und versuchst dann wenigstens die anderen Teilaufgaben selbst zu lösen.
Zu 6a.)
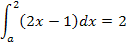
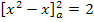
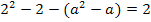
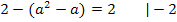
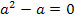
Nun liegt eine gemischtquadratische Gleichung vor, d.h. eine Gleichung mit der Unbekannten zum Quadrat und der Unbekannten hoch 1. Weißt du noch, wie man solche Gleichungen löst? Eine Möglichkeit ist die Verwendung der Mitternachtsformel, doch geht es hier auch wesentlich einfacher. Man kann bei dieser Gleichung nämlich a ausklammern und dann die Faktoren des entstehenden Produkts einzeln gleich Null setzen.
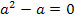
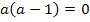
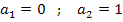
Zu 6b.)
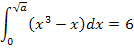
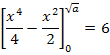
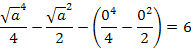
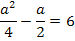
Es liegt jetzt wieder, wie schon in Teilaufgabe 6a.), eine gemischtquadratische Gleichung vor, also eine Gleichung mit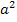 
und a (hoch 1). Doch in diesem Fall hilft das Ausklammern von a nichts. Es würde auf der linken Seite der Gleichung zwar ein Produkt entstehen, wenn man a ausklammert, doch steht auf der rechten Seite die Zahl 6. Es lässt sich nicht eindeutig sagen, wann ein Produkt gleich 6 ist. Da gäbe es unendlich viele Möglichkeiten:
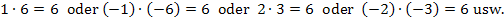
Daher bringt uns hier das Ausklammern von a nicht weiter. (Es wäre nur sinnvoll, wenn auf der rechten Seite der Gleichung eine Null stehen würde.) In diesem Fall müssen wir nun wirklich die Mitternachtsformel anwenden. Bevor wir das machen, multiplizieren wir aber noch mit dem Hauptnenner, also mit der Zahl 4. (Das muss man nicht machen, aber es vereinfacht die Sache, denn dadurch entfallen die Brüche.) Bevor du die Mitternachtsformel anwenden kannst, musst du die Gleichung allerdings auf jeden Fall so umstellen, dass auf einer Seite nur noch eine Null steht.
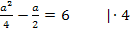
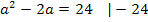
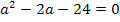
Zur Erinnerung:Gleichungen der Form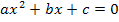 
löst man mit der Mitternachtsformel: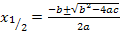 
Bei unserer Gleichung heißt die Variable allerdings nicht x, sondern a. Deshalb schreiben wir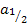 
an Stelle von 
.
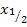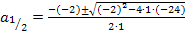
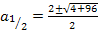
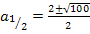
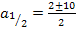
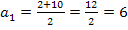
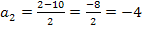
Zu 6c.)
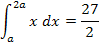
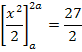
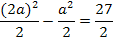
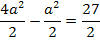
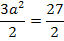
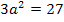
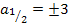
Fertig!
Nun zu einem weiteren Problem:Was tun, wenn man den Wert eines bestimmten Integrals berechnen soll, bei dem sich keine Stammfunktion finden lässt, weil 
zu kompliziert ist?
