3.Volumenberechnungen von Rotationskoerpern mit Hilfe von Integralen
Dadurch ergibt sich eine Gleichung, die als einzig verbliebene Unbekannte a enthält;die anderen Buchstaben R, r und h sind Konstanten, d.h. feste Zahlen, auch wenn wir sie nicht explizit kennen. Wir müssen die Gleichung nach a auflösen. Das bedeutet, dass wir a in Abhängigkeit von R, r und h berechnen können. Die Buchstaben R, r und h werden also noch im Ergebnis für a vorkommen.
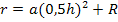
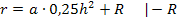
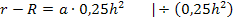
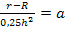
Statt durch 0,25 zu dividieren, kann man auch mit der Zahl 4 multiplizieren. Da 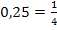 entspricht die Division durch 0,25 auch der Division durch
entspricht die Division durch 0,25 auch der Division durch 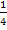 und dies entspricht bekanntlich der Multiplikation mit dem Kehrwert des Bruchs, also der Multiplikation mit
und dies entspricht bekanntlich der Multiplikation mit dem Kehrwert des Bruchs, also der Multiplikation mit 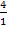 bzw. mit der Zahl 4. So ergibt sich für den Öffnungsfaktor der Parabel:
bzw. mit der Zahl 4. So ergibt sich für den Öffnungsfaktor der Parabel:
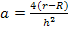
Nun klammern wir im Zähler des Bruchs noch die Zahl -1, also ein Minuszeichen aus. Dadurch dreht sich die Reihenfolge innerhalb der Klammer um. Das Minus ziehen wir dann noch vor den Bruchstrich.
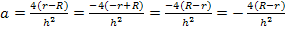
Nun setzen wir das Ergebnis in 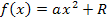 für a ein. So ergibt sich:
für a ein. So ergibt sich:
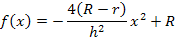
Warum wurde vorher -1 im Zähler ausgeklammert? Ganz einfach! Sonst wären wir nicht auf die in der Angabe vorgegebene Form 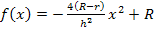 gekommen.
gekommen.
Zu 4b.)
Es soll dasVolumen des Fasses für R = 1, r = 0,6 und h = 2 auf zwei Dezimalen gerundet berechnet werden. Dafür benötigen wir erst einmal die entsprechende Parabelgleichung. Wir setzen daher R = 1, r = 0,6 und h = 2 in 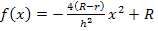 mit x
mit x  [-0,5h| 0,5h] ein:
[-0,5h| 0,5h] ein:
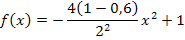
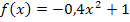
Die Parabelgleichung ist allerdings nur im Intervall [-0,5h| 0,5h] definiert, d.h. im Fall h = 2 gilt:x  [-1| 1]
[-1| 1]
Die Parabel 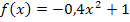 mit x
mit x  [-1| 1] und den zugehörigen Rotationskörper, also das liegende Fass, solltest du selbst in ein Koordinatensystem skizzieren. Wähle dabei den Maßstab nicht zu klein;es bietet sich an auf beiden Achsen 1 LE = 2 cm oder größer zu wählen. (Sonst wird die Zeichnung zu klein.)
[-1| 1] und den zugehörigen Rotationskörper, also das liegende Fass, solltest du selbst in ein Koordinatensystem skizzieren. Wähle dabei den Maßstab nicht zu klein;es bietet sich an auf beiden Achsen 1 LE = 2 cm oder größer zu wählen. (Sonst wird die Zeichnung zu klein.)
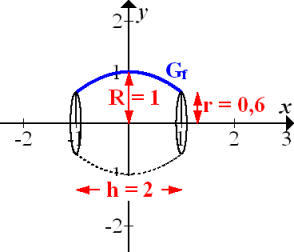
Abb.:Durch Rotation des Graphen  der Funktion
der Funktion 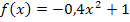 mit x
mit x  [-1| 1] um die x-Achse entsteht ein liegendes Fass mit R = 1, r = 0,6 und h = 2.
[-1| 1] um die x-Achse entsteht ein liegendes Fass mit R = 1, r = 0,6 und h = 2.
Berechnung des Fassvolumens:
Das (liegende) Fass entsteht durch Rotation der Funktion 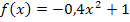 mit x
mit x  [-1| 1] um die x-Achse. Wir können also die oben schon gezeigte Formel für das Volumen von Rotationskörpern bei Rotation von
[-1| 1] um die x-Achse. Wir können also die oben schon gezeigte Formel für das Volumen von Rotationskörpern bei Rotation von  um die x-Achse verwenden:
um die x-Achse verwenden:
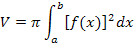
Mit 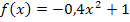 für x
für x  [-1| 1] ergibt sich:
[-1| 1] ergibt sich:
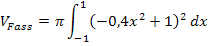
Du kannst das Integral entweder in dieser Form direkt berechnen, also mit den Grenzen -1 und 1, oder du nutzt die Achsensymmetrie der Parabel zur y-Achse aus.

