3.Volumenberechnungen von Rotationskoerpern mit Hilfe von Integralen

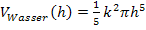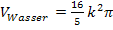Nun setzen wir mit gleich und lösen nach h auf.

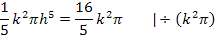
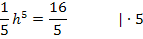
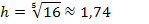
Um die Hälfte des Trichtervolumens mit Wasser zu füllen, muss das Wasser bis auf eine Höhe von ungefähr 1,74 LE eingefüllt werden. Wenn man dies mit der gesamten Trichterhöhe von 2 LE vergleicht, stellt man fest, dass der Wasserspiegel ziemlich hoch stehen muss. Dies ist auf Grund der speziellen Form unseres Trichters nicht verwunderlich. So ist der Trichter, wenn man ihn sich wieder senkrecht aufgerichtet denkt, an seinem oberen Rand schließlich sehr viel breiter als unten;die Trichterbreite nimmt nach oben hin extrem stark zu. Vergleiche dazu noch einmal die Abbildung zu Beginn der Lösung! In der Abbildung ist der Trichter liegend dargestellt. Die schraffierte, ellipsenförmige Fläche in der Abbildung entspricht somit der oberen Öffnung des Trichters, wenn man ihn sich wieder senkrecht aufgerichtet denkt.

4. Bsp.:

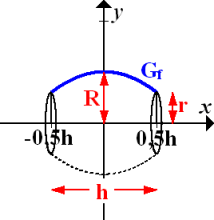
Durch die Rotation eines nach unten geöffneten Parabelbogens mit dem Scheitel (0| R) und den Randpunkten (-0,5h| r) und (0,5h| r) um die x-Achse entsteht ein (liegendes) Fass der Höhe h mit Boden- und Deckelradius r sowie dem Radius R an der breitesten Stelle. Vergleiche Skizze! (R >0, r >0, h >0)

a.) Zeige durch Rechnung, dass der beschriebene Parabelbogen durch die Funktion 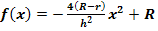mit x [-0,5h| 0,5h] beschrieben wird.

b.) Berechne das Volumen des Fasses für R = 1, r = 0,6 und h = 2 auf zwei Dezimalen gerundet!

c.) Zeige nun allgemein die Gültigkeit der schon von Johannes Keppler gefundenen Formel für das Volumen des Fasses:

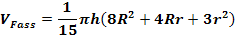
Lösung:

Zu 4a.)

Gezeigt werden soll, dass die gesuchte Parabel durch die Gleichung 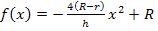mit x [-0,5h| 0,5h] beschrieben wird. Dabei gilt:R >0, r >0, h >0

Wir müssen dazu die Gleichung des oberen Parabelbogens in Abhängigkeit von R, r und h aufstellen. Diese Parabel hat laut Angabe den Scheitel S(0| R) und verläuft durch die Punkte (-0,5h| r) und (0,5h| r). Um die Parabelgleichung aufzustellen benötigen wir nur den Scheitel S(0| R) und einen Kurvenpunkt. Wir verwenden im Folgenden den Punkt (0,5h| r);den zweiten bekannten Kurvenpunkt (-0,5h| r) brauchen wir gar nicht. Wir gehen von der Scheitelform der Parabel aus.

Zur Erinnerung:

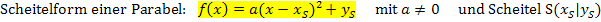
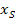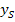Wir setzen zuerst nur die Koordinaten des Scheitels S(0| R) für bzw. ein:

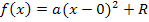
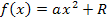
Um den Öffnungsfaktor a zu berechnen, setzen wir nun auch noch die Koordinaten des Punktes (0,5h| r) für x und y ein.

---