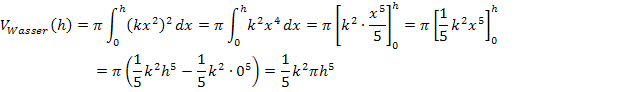3.Volumenberechnungen von Rotationskoerpern mit Hilfe von Integralen
Um das Volumen des eingefüllten Wassers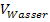 
leichter berechnen zu können, arbeiten wir nun wieder mit dem liegenden Trichter. Nur der liegende Trichter entsteht durch die Rotation um die x-Achse und ausschließlich dafür gilt unsere Formel 
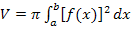. Wir setzen 
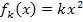wieder in diese Formel ein, integrieren aber nur von 0 bis 1. Im Prinzip handelt es sich daher fast um die gleiche Rechnung wie in Teilaufgabe 3a.) nur mit der oberen Integrationsgrenze 1. Die obere Grenze 1 ergibt sich aus der halben Höhe 1 LE. Wir rechnen dabei, wie schon in Teilaufgabe 3a.), in Abhängigkeit von k. Wir tun einfach so, als wäre k eine feste Zahl, auch wenn wir k nicht kennen.
Berechnung des Volumens des eingefüllten Wassers:
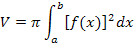
Die Integrationsgrenzen sind a = 0 und b = 1.
Mit 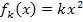ergibt sich für das gesuchte Wasservolumen:
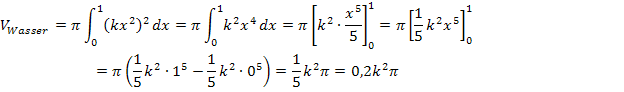
Um den Bruchteil zu berechnen, den das Wasservolumen 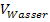am gesamten Trichtervolumen 
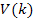einnimmt, brauchen wir nur 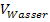durch 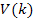zu teilen.
In Teilaufgabe 3a.) haben wir das gesamte Trichtervolumen 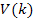schon ermittelt:
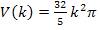
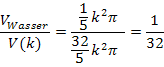
Wenn das Wasser bis zur halben Höhe des Trichters eingefüllt ist, nimmt sein Volumen demnach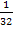 
des gesamten Trichtervolumens ein. Das ist so wenig, nämlich 
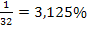, weil der Trichter unten so extrem eng und oben im Vergleich zu unten extrem breit ist. Obwohl das Wasser bis zur Hälfte der Höhe eingefüllt ist, ist nur 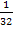des gesamten Trichtervolumens mit Wasser gefüllt.
Zu 3c.)
Der Trichter soll nun zur Hälfe seines Volumens mit Wasser gefüllt werden. Wie hoch muss dazu Wasser eingefüllt werden?
Aus Teilaufgabe 3a.) kennen wir das gesamte Volumen des Trichters: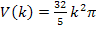 
Die Hälfte des Trichtervolumens soll mit Wasser gefüllt sein. Daher gilt für das Volumen des Wassers: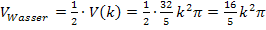 
Nun ist die Frage, wie hoch das Wasser im Trichter steigt, wenn das Wasservolumen genau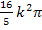 
beträgt.
Um diese Höhe zu ermitteln, müssen wir vorweg das Volumen des Wassers in Abhängigkeit von der (noch unbekannten) Einfüllhöhe h berechnen. Die Einfüllhöhe h entspricht dabei der oberen Integrationsgrenze. Das Wasservolumen in Abhängigkeit von der Einfüllhöhe h bezeichnen wir im Folgenden mit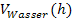 
. Den ermittelten Term für 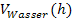werden wir nachher mit dem bekannten Wasservolumen 
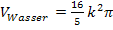gleichsetzen und nach der Höhe h auflösen. So bekommen wir die gesuchte Höhe des Wassers im Trichter.
Versuche das doch gleich alleine durchzurechnen! Zu deiner Kontrolle folgt natürlich der komplette Lösungsweg.
Berechnung des Wasservolumens in Abhängigkeit von der Einfüllhöhe h:
