3.Volumenberechnungen von Rotationskoerpern mit Hilfe von Integralen

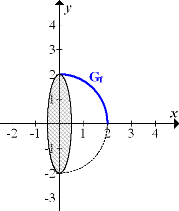
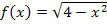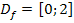Abb.:Der Graph der Funktion mit rotiert um die x-Achse.

Volumenberechnung des Rotationskörpers:

Zuerst berechnen wir das gesuchte Volumen mit Hilfe der Integralrechnung. Wir verwenden die folgende Formel:

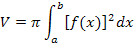
Die Integrationsgrenzen sind durch die Definitionsmenge 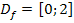festgelegt.

Es gilt:a = 0 und b = 2

Mit 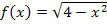ergibt sich:

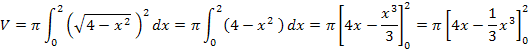
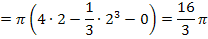
Nun überprüfen wir das Ergebnis, indem wir das Volumen V mit Hilfe der Formel für das Volumen einer Kugel berechnen. Wir suchen allerdings das Volumen einer Halbkugel, daher muss natürlich die Hälfte des gesamten Kugelvolumens genommen werden.

Zur Erinnerung:

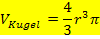
(Diese Formel findest du auch in deiner Formelsammlung bzw. Merkhilfe.)

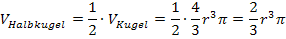
Mit r = 2 ergibt sich:

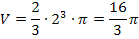
Wir erhalten das gleiche Ergebnis;d.h. die Rechnung stimmt!

3. Bsp.:

Gegeben ist die Funktionenschar 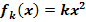mit x [0;2] und k >0. Ihre Graphen werden mit 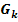bezeichnet.

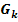rotiert um die x-Achse;dadurch entsteht ein trichterförmiger Rotationskörper.

a.) Berechne das Volumen dieser Rotationskörper in Abhängigkeit von k.

b.) Der Trichter wird bis zur halben Höhe mit Wasser gefüllt. Welchen Bruchteil des gesamten Trichtervolumens nimmt dabei das Wasser ein?

c.) Der Trichter soll nun zur Hälfe seines Volumens mit Wasser gefüllt werden. Wie hoch muss dazu das Wasser eingefüllt werden?

Lösung:

Gegeben ist die Schar quadratischer Funktionen 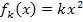mit x [0;2] und k >0. Es handelt sich also um eine Schar von Parabeln. Da der Scharparameter k laut Angabe immer positiv ist, sind alle Parabeln nach oben geöffnet. Alle haben ihren Scheitel im Ursprung.

Damit du dir das Ganze besser vorstellen kannst, solltest du dir eine Skizze wenigstens eines der Graphen 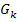machen. Dazu musst du natürlich eine konkrete Zahl für den Scharparameter k wählen. Wir entscheiden uns der Einfachheit wegen für k = 1. Dann ergibt sich 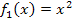. Der Graph 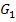ist ein Teil der nach oben geöffneten Normalparabel mit dem Scheitel S(0|0). Achtung:Wegen x [0;2] darfst du nur den Teil von x = 0 bis x = 2 des steigenden Astes der Normalparabel zeichnen.

Nun stellen wir uns vor, dass der Graph 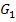um die x-Achse rotiert. Um den zugehörigen Rotationskörper zu skizzieren, spiegelst du zuerst den Graph 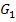an der x-Achse und verbindest dann die rechten Randpunkte mit einer schmalen Ellipse. Es ergibt sich dadurch ein trichterförmiger Rotationskörper. Siehe folgende Abbildung!

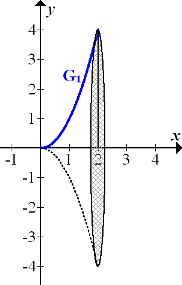
Abb.:Der Graph 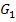der Funktion 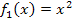mit x [0;2] rotiert um die x-Achse.

---