3.Volumenberechnungen von Rotationskoerpern mit Hilfe von Integralen
Merkhilfe.)
Mit r = 3 und h = 6 ergibt sich:
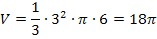
Wir erhalten das gleiche Ergebnis;d.h. die Rechnung stimmt!
Zu 2b.)
Zuerst müssen wir den Graph der Funktion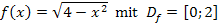 
zeichnen. Vermutlich kannst du dir nicht sofort vorstellen, wie dieser Graph aussieht. Du könntest ihn natürlich mit Hilfe einer kleinen Wertetabelle zeichnen, doch ist dies nicht so elegant und ohne Taschenrechner nur für sehr wenige Werte machbar. (Beachte dabei, dass du nur Zahlen von 0 bis 2 für x einsetzen darfst.) Eine Wertetabelle ist hier an sich völlig unnötig, denn es handelt sich um einen Viertelkreis um den Ursprung mit Radius r = 2, der im I. Quadranten liegt. Nun stellt sich dir vermutlich die Frage, woher man das wissen kann. Dazu müssen wir vorweg erklären, warum die Gleichung 
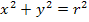einen Kreis um den Ursprung mit Radius r beschreibt. Betrachte dazu die nachfolgende Abbildung!
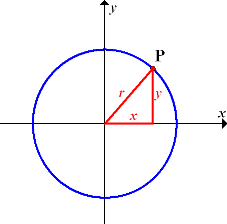
Abb.:Die Punkte P(x|y) liegen auf einem Kreis mit M(0|0) und Radius r
Für jeden Punkt P(x|y) der Kreislinie gilt der Satz des Pythagoras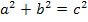 
. Dabei entsprechen den Katheten a und b in unserem Fall x und y. Der Hypotenuse c entspricht bei uns der Radius r. (r liegt gegenüber des rechten Winkels und ist daher die Hypotenuse. Zwischen der Abszisse x und der Ordinate y ist zwangsläufig ein rechter Winkel, da wir in einem kartesischen Koordinatensystem arbeiten.) Es gilt somit für alle Punkte P(x|y) des Kreises k um M(0|0) mit dem Radius r die folgende Gleichung:
Wenn wir die Kreisgleichung nach y auflösen, ergibt sich:
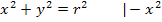
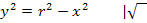
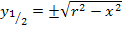
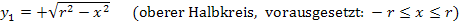
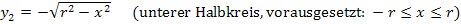
Wenn du nun die Funktion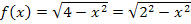 
mit 
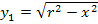vergleichst, wirst du feststellen, dass die Zahl 2 bei 
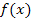dem Radius r entspricht. 
ist somit ein Teil des oberen Halbkreises um den Ursprung mit Radius 2. Warum nicht der ganze obere Halbkreis? Wegen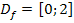 
dürfen nur die Zahlen von 0 bis 2 für x eingesetzt werden. Wenn keine negativen Zahlen für x eingesetzt werden dürfen, kann der Graph nicht links von der y-Achse verlaufen. Daher ist der Graph nur ein Viertelkreis im I. Quadranten und nicht der ganze obere Halbkreis. (Um den linken oberen Viertelkreis zu erhalten, müsste gelten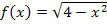 
mit x 
[-2|0]. Den gesamten oberen Halbkreis erhielte man für 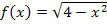mit x [-2|2]. Also immer schön auf die Definitionsmenge achten!)
Jetzt kannst du den Graph der Funktion 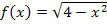mit 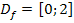leicht zeichnen. Dann lassen wir in Gedanken um die x-Achse rotieren. Skizzieren kannst du das am besten, indem du zuerst an der x-Achse spiegelst und dann die linken Randpunkte durch eine schmale Ellipse verbindest. Es entsteht eine Halbkugel. Betrachte dazu die folgende Abbildung!
