3.Volumenberechnungen von Rotationskoerpern mit Hilfe von Integralen

Außerdem gilt bekanntlich: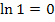

Damit können wir schreiben:

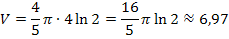
Wir erhalten natürlich das gleiche Ergebnis wie schon bei der 1. Methode. Das Werkstück besitzt ein Volumen von .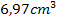

Berechnung der Masse:

Nachdem wir V berechnet haben, können wir leicht die gesuchte Masse berechnen.

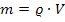
Die Dichte ist mit 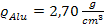gegeben;wir müssen nur noch das Volumen 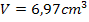und die Dichte einsetzen.

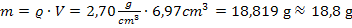
Fertig!

Dies soll uns an Beispielen für die Volumenberechnung von Rotationskörpern reichen. Es handelt sich dabei sowieso nur um ein Randthema im Mathe-Abitur.

---