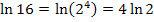3.Volumenberechnungen von Rotationskoerpern mit Hilfe von Integralen
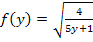
Jetzt kann in die Formel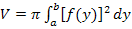 
eingesetzt werden. Mit a = 0 und b = 3 ergibt sich:
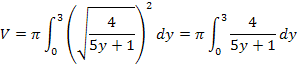
Das vorliegende Integral kann mit Hilfe der folgenden Integrationsregel gelöst werden.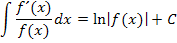 
Siehe auch:Weitere Integrationsregeln
Du musst dir dabei natürlich statt dem x in der Integrationsregel jeweils ein y denken, da wir hier schließlich nach dy integrieren. Außerdem passt der Zähler bei unserem Integral noch nicht ganz. Die Ableitung des Nenners ist nicht 4, sondern 5. Daher brauchen wir noch einen Korrekturfaktor vor dem Integral, damit im Zähler dann die Zahl 5, also die Ableitung des Nenners zu stehen kommt. (Wie man am leichtesten auf den benötigten Faktor kommt, den man vor das Integral schreiben muss, damit im Zähler die Ableitung des Nenners zu stehen kommt, wird ausführlich erklärt im Teil:Weitere Integrationsregeln)
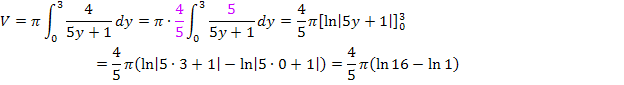
Statt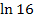 
kann man auch mit Hilfe des Logarithmus-Rechengesetzes 
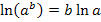etwas schöner 
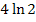schreiben: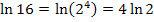 
Außerdem gilt bekanntlich: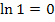 
Damit können wir schreiben:
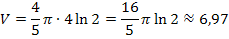
Laut Angabe gilt:1 LE = 1 cm
Das Volumen ist somit in der Einheit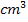 
berechnet worden und das Werkstück besitzt ein Volumen von 
.
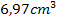2. Methode
Wir ermitteln zuerst die Umkehrfunktion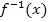 
zu der Funktion 
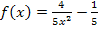. Dazu vertauschen wir vorweg x gegen y und lösen dann wieder nach y auf.
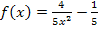
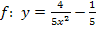
Vertauschen von x gegen y liefert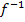 
:
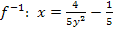
Auflösen nach y:
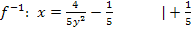
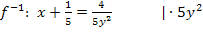
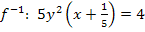
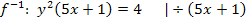
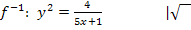
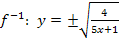
Da laut Angabe gilt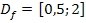 
ist entsprechend auch die Wertemenge der Umkehrfunktion 
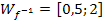. (Bekanntlich gilt: 
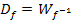) Die Funktionswerte der Umkehrfunktion 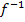liegen also zwischen 0,5 und 2. Somit können bei der Umkehrfunktion 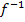keine negativen Werte herauskommen und deshalb entfällt das Minuszeichen vor der Wurzel. Die Gleichung der Umkehrfunktion lautet:
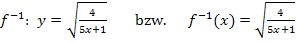
Nun kann in die Formel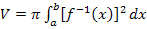 
eingesetzt werden. Mit a = 0 und b = 3 ergibt sich:
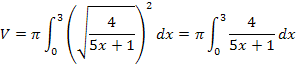
Das vorliegende Integral kann mit Hilfe der folgenden Integrationsregel gelöst werden.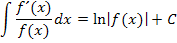
Leider passt der Zähler bei unserem Integral noch nicht ganz, er ist nur ein Vielfaches der Nennerableitung, aber nicht exakt die Ableitung des Nenners. Die Ableitung des Nenners ist nicht 4, sondern 5. Daher brauchen wir noch einen Korrekturfaktor vor dem Integral, damit im Zähler dann die Zahl 5, also die Ableitung des Nenners zu stehen kommt. (Wie man am leichtesten auf den benötigten Faktor kommt, den man vor das Integral schreiben muss, damit im Zähler die Ableitung des Nenners zu stehen kommt, wird ausführlich erklärt im Teil:Weitere Integrationsregeln)
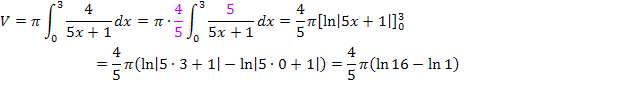
Statt 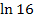kann man auch mit Hilfe des Logarithmus-Rechengesetzes 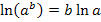etwas schöner 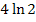schreiben:
