3.Volumenberechnungen von Rotationskoerpern mit Hilfe von Integralen
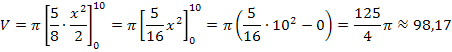
Wir erhalten natürlich dasselbe Ergebnis wie bei der Berechnung nach der 1. Methode.
Es folgt ein weiteres Beispiel zur Volumenberechnung bei Rotation eines Funktionsgraphen um die y-Achse. Versuche die Aufgabe zuerst alleine zu lösen, bevor du dir die Lösung anschaust!
2. Bsp.:
Gegeben ist die Funktion 
. Der Graph 
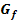rotiert um die y-Achse. Dadurch entsteht ein rotationssymmetrisches Werkstück, das vollständig aus Aluminium gegossen werden soll. Für beide Achsen gilt:1 LE = 1 cm
Welche Masse hat dieses Werkstück?
Hinweis:Dichte von Aluminium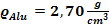 
Lösung:
Aus der Physik kennst du die Formel für die Dichte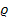 
eines Körpers:
Dabei steht m für die Masse des Körpers und V für sein Volumen. Die Dichte 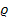ist eine Materialkonstante, also eine feste Zahl, die je nach Material des Körpers unterschiedlich ist. Der Angabe ist zu entnehmen, dass für Aluminium gilt: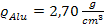 
Es soll die Masse m des Werkstücks berechnet werden. Daher stellen wir die Formel entsprechend um.
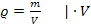
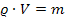
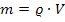
Die Dichte ist mit 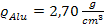gegeben, wir müssen aber noch das Volumen V vorweg berechnen, um nachher die Masse m ermitteln zu können.
Zur Berechnung des Volumens:
Der Graph der Funktion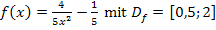 
rotiert um die y-Achse. Damit wir wissen, von wo bis wo wir integrieren müssen, brauchen wir die Wertemenge 
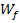, d.h. die y-Koordinaten der Randpunkte. (Die Funktion ist für x 
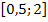streng monoton fallend. Der kleinstmögliche x-Wert führt somit zum größtmöglichen y-Wert und entsprechend der größtmögliche x-Wert zum kleinstmöglichen y-Wert.)
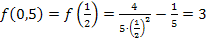
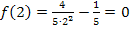
Somit gilt für die Wertemenge: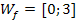 
Wir müssen auf jeden Fall von 0 bis 3 integrieren, egal nach welcher Methode vorgegangen werden soll.
Damit du dir das Ganze besser vorstellen kannst, solltest du dir eine Skizze dazu anfertigen. Sie könnte folgendermaßen aussehen:
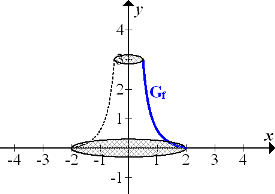
Abb.:Durch Rotation des Graphen 
der Funktion 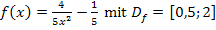um die y-Achse entsteht ein rotationssymmetrisches Werkstück. Grund- und Deckfläche des Werkstücks sind schraffiert dargestellt.
Im Folgenden werden beide Methoden der Volumenberechnung des Rotationskörpers gezeigt. Für dich reicht es natürlich, wenn du einen Weg komplett durchgerechnet hast. Dann kannst du deine eigene Lösung Schritt für Schritt mit der jeweiligen Musterlösung vergleichen.
1. Methode
Auflösen von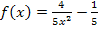 
nach x ergibt:
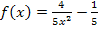
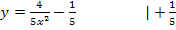
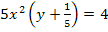
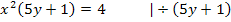
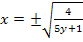
Das Minuszeichen entfällt hier, da laut Definitionsmenge x keine negativen Werte annehmen kann.
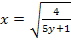
Nun liegt die Funktion in der nach x aufgelösten Form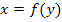 
vor.
