3.Volumenberechnungen von Rotationskoerpern mit Hilfe von Integralen

1. Bsp.:

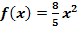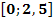Der Kelch eines Sektglases entsteht durch Rotation der Funktion mit x um die y-Achse.  Auf beiden Achsen gilt:1 LE = 1 cm

Berechne die Höhe und das Volumen des Sektkelchs!

Lösung:

Obwohl es nicht verlangt ist, fertigen wir eine Zeichnung an, die den Graph der Funktion 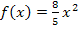mit x 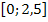zeigt. Es handelt sich bei um ein Stück des steigenden Astes einer nach oben geöffneten Parabel mit Scheitel im Ursprung, die etwas schmäler ist als die Normalparabel. (Für eine exakte Zeichnung brauchst du eine Wertetabelle.) Dann stellen wir uns vor, dass der Graph um die y-Achse rotiert. So entsteht der Sektkelch. (Stiel und Fuß  des Sektglases muss man sich dazu denken.) Den Rotationskörper kannst du am besten in das Koordinatensystem skizzieren, indem du den Graph an der y-Achse spiegelst und die beiden oberen Randpunkte mit einer schmalen Ellipse verbindest. Vergleiche dazu die folgende Abbildung!

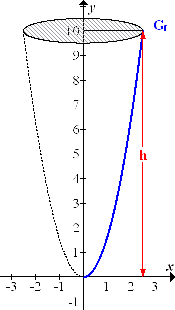
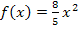Abb. Durch die Rotation des Graphen der Funktion mit x 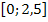um die y-Achse entsteht ein Sektkelch (ohne Stiel und Fuss).

Die Höhe des Sektkelchs ergibt sich aus der Differenz der y-Koordinaten der Randpunkte der Funktion 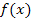. Laut Angabe gilt:x

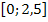
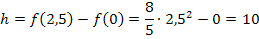
Wegen 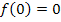entspricht die Höhe des Sektkelchs hier einfach der y-Koordinate des rechten Randpunktes. Du kannst die Höhe also auch direkt mit 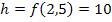berechnen.

Laut Angabe gilt:1 LE in der Zeichnung entspricht 1 cm in der Realität;d.h. die Höhe des Sektkelchs beträgt 10 cm.

Der Sektkelch entsteht durch Rotation des Graphen um die y-Achse. Um das Volumen des Sektkelchs zu ermitteln, verwenden wir die oben beschriebene 1. Methode für Rotation um die y-Achse.

·        Auflösen der Funktion 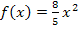nach x ergibt :

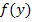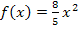
Statt 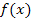schreiben wir 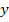und lösen dann nach x auf.

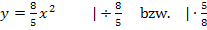
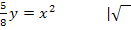
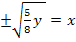
Wegen x 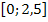fällt das Minus weg;x muss schließlich positiv sein und nur eine Wurzel mit Plus davor ist positiv. Daher gilt:

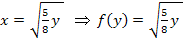
·        Einsetzen in die Formel für die Rotation eines Graphen um die y-Achse:

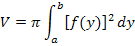
Der Sektkelch ist unten durch 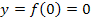und oben durch 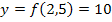begrenzt. Somit müssen wir von 0 bis 10 integrieren. Betrachte dazu noch einmal die obige Abbildung!

Mit 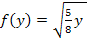ergibt sich:

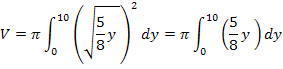
Integration nach dy liefert:

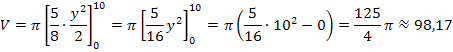
Hinweis:Beim Integrieren nach dy musst du dich ausschließlich auf die Potenzen von y konzentrieren. Nur bei den y-Potenzen musst du 1 dazuzählen und durch den neuen Exponenten teilen. Das geht im Prinzip ähnlich wie beim Integrieren nach dx;dabei konzentriert man sich ausschließlich auf die Potenzen von x.

---