3.Volumenberechnungen von Rotationskoerpern mit Hilfe von Integralen
Nicht klar? Ok, dann ganz langsam. Eine lineare Funktion mit der Steigung m und dem y-Achsenabschnitt t hat die allgemeine Gleichung y = mx + t . Da unsere Gerade waagrecht verläuft, ist die Steigung m = 0. Außerdem soll die Gerade die y-Achse bei r schneiden;deshalb ist der y-Achsenabschnitt t = r. Eingesetzt in die allgemeine Geradengleichung ergibt sich:y = 0x + r bzw. y = r. Statt y kann man auch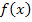 
schreiben. So kommt man auf die Gleichung 
.
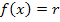Für x 
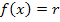ℝwäre der Graph der Funktion eine unendlich lange Gerade, welche die y-Achse bei r schneidet. Wir brauchen aber nur ein Stück der Geraden;es soll die Länge h besitzen. Daher müssen wir die Definitionsmenge entsprechend einschränken. Die x-Werte müssen zwischen x = 0 und x = h liegen, damit sich bei der Rotation von 
ein Zylinder der Höhe h ergibt. (Theoretisch könnte man auch mit einem zur Seite verschobenen Zylinder arbeiten, beispielsweise um 1 nach rechts verschoben. Dann wäre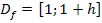 
und man müsste nachher von 1 bis 1 + h integrieren. Dass wäre jedoch umständlicher zu rechnen, weil die untere Integrationsgrenze dann nicht mehr 0 wäre.)
Daher arbeiten wir lieber mit den Grenzen 0 und h, also mit 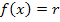in der Definitionsmenge 
.
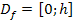Durch die Rotation von um die x-Achse entsteht ein liegender Zylinder mit der Höhe h und dem Radius r. Betrachte dazu noch einmal unsere Skizze!
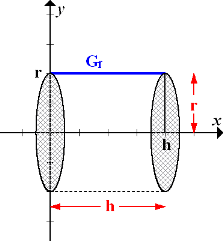
Abb.:Die blaue Gerade hat die Gleichung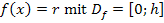 
. Ihr Graph rotiert um die x-Achse. Dadurch entsteht ein Zylinder mit der Höhe h und dem Radius r.
Das Volumen unseres Zylinders lässt sich mit der Formel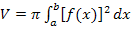 
berechnen, da er durch Rotation von um die x-Achse entsteht.
Mit a = 0 und b = h ergibt sich:
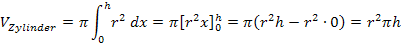
Somit haben wir die Formel für das Volumen eines Zylinders hergeleitet.
Dir ist der erste Schritt der Integration nicht klar? Warum gilt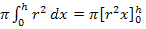 
? Lassen wir das 
mal weg und überlegen uns, wie man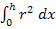 
berechnet. Es soll nach dx integriert werden;d.h. x ist die Variable und nicht etwa r. Wir integrieren schließlich nicht nach dr! Das Dumme ist nur, dass gar kein x im Integranden vorkommt. Der Integrand ist hier ja 
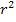. Dies ist eine Konstante;da r konstant ist, ist auch 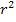konstant. 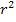ist deshalb wie eine ganz normale Zahl (ohne x) zu behandeln. Denke nun einmal kurz darüber nach, wie du eine normale Zahl nach dx integrieren würdest! Was wäre zum Beispiel 
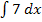oder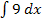 
?
Das Integrieren ist ja das Gegenteil des Ableitens. Die Frage ist also, welche Funktion abgeleitet wieder 7 bzw. 9 ergibt. Du weißt sicher, dass 7x abgeleitet 7 ergibt, und entsprechend, dass 9x abgeleitet 9 ist.
