3.Volumenberechnungen von Rotationskoerpern mit Hilfe von Integralen

Der Ausdruck innerhalb der Klammer wird auf einen gemeinsamen Bruchstrich geschrieben:

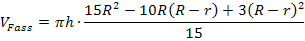
Statt durch 15 zu teilen, kann man auch mit 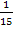multiplizieren. (Da ein Bruchstrich wie eine Klammer wirkt, muss dann aber eine Klammer um den Ausdruck gesetzt werden, der vorher im Zähler stand. Deshalb ist die eckige Klammer in der nächsten Zeile nötig.)

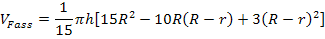
Vereinfachung des Ausdrucks in der eckigen Klammer durch Ausmultiplizieren von 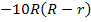und Anwendung der zweiten binomischen Formel bei :

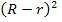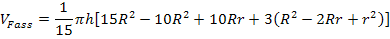
Auflösen der runden Klammer;die Zahl 3 wird in die runde Klammer hineinmultipliziert:

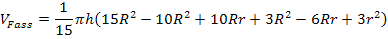
Zusammenfassen soweit möglich:

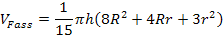
Super! Das ist genau die Formel, die gezeigt werden sollte. Wir sind endlich fertig!

5. Bsp.:Herleitung der Volumenformeln für Zylinder und Kegel

a.) Leite mit Hilfe der Integralrechnung die Formel für das Volumen eines geraden Kreiszylinders mit der Höhe h und dem Radius r her!

b.) Leite mit Hilfe der Integralrechnung die Formel für das Volumen eines geraden Kreiskegels mit der Höhe h und dem Radius r her!

Lösung:

Die Buchstaben r und h, die für Radius bzw. Höhe stehen, sind Konstanten. D.h. sie sind wie feste Zahlen zu behandeln, obwohl wir r und h nicht explizit kennen.

In den folgenden Teilaufgaben gilt:r >0 und h >0

(Es handelt sich schließlich sowohl bei r als auch bei h jeweils um eine Streckenlänge und eine Streckenlänge kann nicht negativ oder gleich Null sein.)

Du weißt nicht, was mit „gerader Kreiszylinder“ und mit „gerader Kreiskegel“ gemeint ist? Ganz einfach:Ein gerader Kreiszylinder ist ein ganz normaler Zylinder mit kreisförmiger Grund- und Deckfläche, wobei die Mantelfläche senkrecht zur Grund- und Deckfläche verläuft. Ein gerader Kreiskegel ist entsprechend ein ganz normaler Kegel mit kreisförmiger Grundfläche, bei dem die Spitze senkrecht über dem Mittelpunkt der Grundfläche liegt.

Zu 5a.)

Herleitung der Zylinderformel: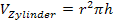

Zuerst brauchen wir eine geeignete Funktion 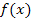, die bei Rotation um die x-Achse einen Zylinder mit Radius r und der Höhe h ergibt. Wir nehmen eine waagrechte Gerade, welche die y-Achse bei r schneidet, und lassen sie um die x-Achse rotieren. Siehe Skizze!

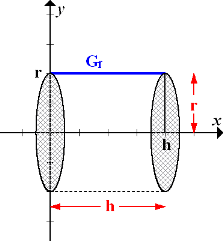
Abb.:Der Graph rotiert um die x-Achse. Dadurch entsteht ein Zylinder mit der Höhe h und dem Radius r.

Überlege dir nun, wie die Gleichung der Geraden 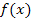lauten muss!

Hoffentlich bist du selbst darauf gekommen, dass die benötigte Gerade die Gleichung 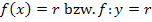hat.

---