3.Volumenberechnungen von Rotationskoerpern mit Hilfe von Integralen
Wir lassen den Graph einer gegebenen Funktion um eine der Koordinatenachsen rotieren. Je nach dem, um welche Achse der Graph rotiert, ergeben sich dabei verschiedene Rotationskörper. Wie lässt sich das Volumen eines solchen Rotationskörpers ermitteln? Wir beginnen mit dem einfacheren der beiden Fälle, der Rotation um die x-Achse. Der zweite Fall, die Rotation um die y-Achse, kann durch Verwendung der Umkehrfunktion auf die Rotation um die x-Achse zurückgeführt werden. Dazu erst weiter unten mehr.
3.1 Rotation um die x-Achse
Gegeben ist Funktion 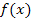 mit der Definitionsmenge
mit der Definitionsmenge 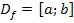 . Ihr Graph
. Ihr Graph  rotiert um die x-Achse. Dadurch entsteht ein Rotationskörper. Vergleiche Skizze!
rotiert um die x-Achse. Dadurch entsteht ein Rotationskörper. Vergleiche Skizze!
![]()
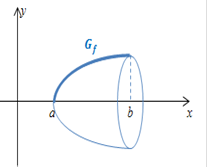
Abb.:Der Graph  (dick dargestellt) rotiert um die x-Achse;es entsteht ein Rotationskörper, der in diesem Beispiel einem liegenden Sektglas (ohne Stiel und Fuß) ähnelt.
(dick dargestellt) rotiert um die x-Achse;es entsteht ein Rotationskörper, der in diesem Beispiel einem liegenden Sektglas (ohne Stiel und Fuß) ähnelt.
Mit Hilfe der folgenden Formel lässt sich das Volumen des entstehenden Rotationskörpers berechnen:
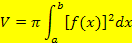
Herleiten lässt sich diese Formel, indem man sich den Rotationskörper in unendlich viele, extrem schmale Scheibchen zerteilt denkt. Wir schneiden jeweils im Abstand 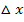 senkrecht zur x-Achse. Wählt man
senkrecht zur x-Achse. Wählt man 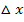 sehr klein, entstehen viele kleine Scheibchen, die wir näherungsweise als Zylinder mit der Höhe
sehr klein, entstehen viele kleine Scheibchen, die wir näherungsweise als Zylinder mit der Höhe 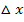 ansehen können. Der Radius der Zylinder entspricht
ansehen können. Der Radius der Zylinder entspricht 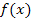 . Betrachte
. Betrachte
dazu die folgende Abbildung!
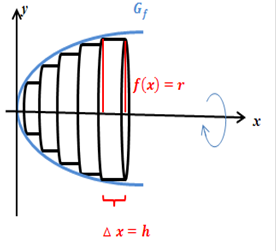
Bekanntlich wird das Volumen eines Zylinders mit der Formel 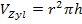 berechnet, wobei r für den Radius und h für die Höhe des Zylinders stehen.
berechnet, wobei r für den Radius und h für die Höhe des Zylinders stehen.
Mit 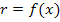 und
und 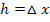 ergibt sich für das Volumen eines einzelnen Zylinders, der unserem Rotationskörper einbeschrieben ist:
ergibt sich für das Volumen eines einzelnen Zylinders, der unserem Rotationskörper einbeschrieben ist:
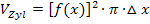
Addiert man die Volumina der einzelnen Zylinder, ergibt sich logischerweise das Gesamtvolumen. Nun stellen wir uns vor, dass wir dabei die Höhe der Einzelzylinder gegen Null gehen lassen;d.h. wir machen 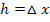 immer kleiner. Dann nähert sich die Summe der Volumina aller Einzelzylinder dem Volumen des gesamten Rotationskörpers an. Die Summe entspricht dabei dem Integral. (Warum das so ist, wird ausführlich erklärt im Teil:Die Streifenmethode)
immer kleiner. Dann nähert sich die Summe der Volumina aller Einzelzylinder dem Volumen des gesamten Rotationskörpers an. Die Summe entspricht dabei dem Integral. (Warum das so ist, wird ausführlich erklärt im Teil:Die Streifenmethode)
Auf eine genaue Herleitung der Formel 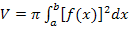 wollen wir hier verzichten, da du sie nicht wirklich brauchst. Außerdem ist dir vermutlich die Schreibweise mit dem Summenzeichen
wollen wir hier verzichten, da du sie nicht wirklich brauchst. Außerdem ist dir vermutlich die Schreibweise mit dem Summenzeichen 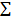 nicht geläufig. Daher belassen wir es hier bei der Feststellung, dass sich die Summe der Volumina aller n Einzelzylinder auch folgendermaßen schreiben lässt:
nicht geläufig. Daher belassen wir es hier bei der Feststellung, dass sich die Summe der Volumina aller n Einzelzylinder auch folgendermaßen schreiben lässt:
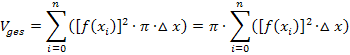
Dabei stellt n die Anzahl der einzelnen Zylinder dar. Wenn wir die Höhe der einzelnen Zylinder 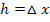 immer kleiner machen, wächst entsprechend die Anzahl n der einzelnen Zylinder. Geht
immer kleiner machen, wächst entsprechend die Anzahl n der einzelnen Zylinder. Geht 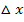 gegen Null, geht umgekehrt n gegen Unendlich. Die Summe der Volumina dieser unendlich vielen Zylinder mit extrem kleiner Höhe führt uns zum Volumen V des gesuchten Rotationskörpers.
gegen Null, geht umgekehrt n gegen Unendlich. Die Summe der Volumina dieser unendlich vielen Zylinder mit extrem kleiner Höhe führt uns zum Volumen V des gesuchten Rotationskörpers.
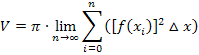
Wie gesagt, wird hier auf die exakte mathematische Herleitung der Formel des Volumens von Rotationkörpern verzichtet. Sie ist ziemlich lang und kompliziert.

