2. Berechnungen von Mittelwerten mit Hilfe von Integralen
Wir müssen also zuerst eine Stammfunktion zu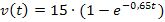 
finden und nachher die Grenzen einsetzen.
Die Zahl 15 ist eine multiplikative Konstante, d.h. eine Zahl ohne der Variablen t, mit der multipliziert wird;die Zahl 15 wird daher beim Integrieren einfach abgeschrieben. Die Zahl 1 ist eine additive Konstante, d.h. eine Zahl ohne Variable mit Plus oder Minus;Beim Integrieren nach t kommt ein t dazu. (Siehe auch:Die Stammfunktion F(x) und einfache Integrationsregeln) Das Schwierigste beim Integrieren ist hier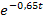 
;es handelt sich dabei um eine linear transformierte Funktion, d.h. um eine e-Funktion, bei der statt der Variablen eine lineare Funktion, also eine Geradengleichung, eingesetzt ist. Besser erkennt man das, wenn man sich 
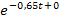denkt. Im Exponenten steht die lineare Funktion 
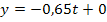. Denke dir außerdem an Stelle des Buchstabens t den Buchstaben x, das macht dir die Sache etwas einfacher. Dann kannst du die Formel 
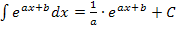anwenden. In der Formelsammlung bzw. Merkhilfe steht diese Formel leider nicht. Auf der Merkhilfe für G8 findest du zumindest die allgemeine Formel für lineartransformierte Funktionen 
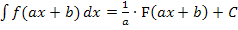. (Siehe auch:Weitere Integrationsregeln)
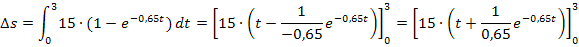
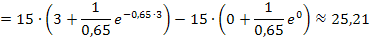
Der Körper durchfällt innerhalb der ersten drei Sekunden einen Weg von ungefähr 25,21 m.
Zu 3b.)
Gesucht ist die mittlere Geschwindigkeit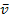 
innerhalb der ersten drei Sekunden. Wir suchen also diejenige (konstante) Geschwindigkeit, mit welcher der Körper innerhalb der ersten drei Sekunden den gleichen Weg 
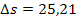m durchfallen würde.
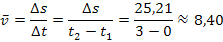
Du kannst stattdessen natürlich auch mit der Formel für die mittlere Geschwindigkeit arbeiten:
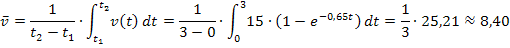
Die mittlere Geschwindigkeit des Körpers innerhalb der ersten drei Sekunden beträgt demnach ungefähr 8,40 m/s.
Zu 3c.)
Es ist die mittlere Geschwindigkeit 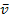innerhalb der zweiten bis zur fünften Sekunde gesucht.
