2. Berechnungen von Mittelwerten mit Hilfe von Integralen
Innerhalb der Zeitspanne von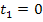 
bis 
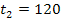legt das Auto die Strecke 
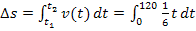zurück. Vergleiche dazu die grün schraffierte Fläche in der folgenden Abbildung!
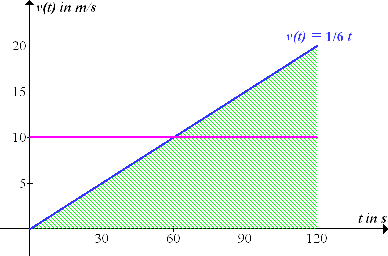
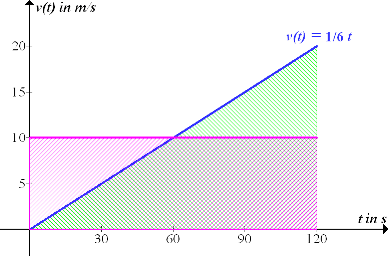
Abb.:Zeit-Geschwindigkeitsfunktion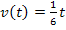 
und mittlere Geschwindigkeit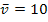 
Würde das Auto konstant mit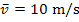 
fahren, würde es ebenfalls in 120 Sekunden den gleichen Weg 
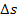zurücklegen. Man erkennt dies in der Graphik daran, dass die grün schraffierte Fläche genauso großist wie die rechteckige, rosa schraffierte Fläche. Betrachte dazu die nächste Abbildung! (Das ausschließlich rosa schraffierte Dreieck ist genauso großwie das ausschließlich grün schraffierte Dreieck.)
Wie wurde aber die mittlere Geschwindigkeit 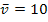berechnet? Wir suchten nach einer konstanten Geschwindigkeit 
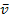, mit der innerhalb von 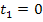bis 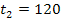der Weg 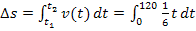zurückgelegt würde. Mit der Formel 
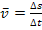ergibt sich daher:
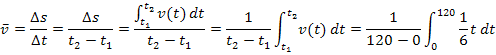
Das ist natürlich genau die Formel, mit der wir gearbeitet haben. Hoffentlich ist dir nun klar, warum die Formel gilt.
Nach dem gleichen Prinzip können auch andere Mittelwerte berechnet werden, zum Beispiel der Mittelwert einer Temperatur oder einer Kraft. Dazu muss logischerweise die entsprechende Funktion bekannt sein, welche den Zusammenhang zwischen Zeit und vorherrschender Temperatur bzw. Zeit und wirkender Kraft beschreibt. Schauen wir uns auch dazu ein konkretes Beispiel an.
2. Bsp.:
Die Funktion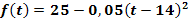 
mit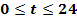 
beschreibt die Temperatur in °C, wobei t für die Uhrzeit in Stunden steht. (t = 0 entspricht 0 Uhr und 
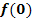die zugehörige Temperatur in °C.)
a.) Berechne die mittlere Tagestemperatur!
b.) Berechne die mittlere Temperatur zwischen 8 Uhr und 18 Uhr!
Lösung:
Zu 2a.)
Unter der mittleren Tagestemperatur versteht man die mittlere Temperatur innerhalb von 24 Stunden, also von 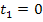bis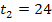 
. Wir bezeichnen die mittlere Tagestemperatur mit 
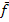. Sie wird ähnlich wie die mittlere Geschwindigkeit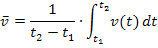 
berechnet, d.h. wir arbeiten mit der folgenden Formel:
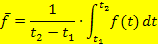
Mit der angegebenen Zeit-Temperaturfunktion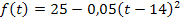 
ergibt sich:
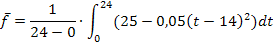
Um das Integral leichter berechnen zu können, vereinfachen wir vorweg die Funktion 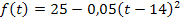. Wir quadrieren die Klammer mit Hilfe der zweiten binomischen Formel 
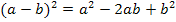, multiplizieren danach den Faktor -0,05 in die Klammer hinein und fassen soweit möglich zusammen.
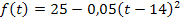
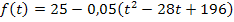
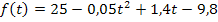
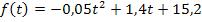
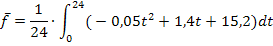
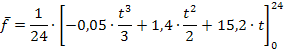
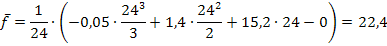
Die mittlere Tagestemperatur beträgt demnach 22,4 °C.
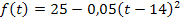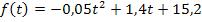Damit du dir das Ganze besser vorstellen kannst, wird der Graph der Zeit-Temperaturfunktion bzw. für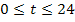 
in der folgenden Abbildung gezeigt.
