2. Berechnungen von Mittelwerten mit Hilfe von Integralen
Für die mittlere (durchschnittliche) Geschwindigkeit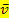 
gilt:
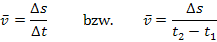
Mit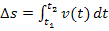 
ergibt sich:
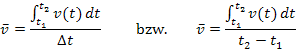
Oder anders geschrieben:
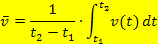
Das sieht für dich jetzt wahrscheinlich kompliziert aus, aber keine Angst, es ist eigentlich gar nicht so schlimm. Die Zeitpunkte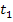 
und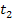 
, sowie die Funktion 
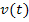sind in konkreten Aufgaben angegeben. Du brauchst nur noch in die Formel einzusetzen, um den Mittelwert zu berechnen. Am besten schauen wir uns gleich ein konkretes Beispiel an.
1. Bsp.:
Ein Auto beschleunigt konstant innerhalb von 2 Minuten von 0 auf 20 m/s. Seine Geschwindigkeit v (in m/s) nach t Sekunden ab dem Start wird durch die Funktion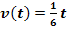 
für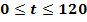 
beschrieben.
Mit welcher (konstanten) Geschwindigkeit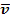 
müsste das Auto fahren, damit es innerhalb der gleichen Zeitspanne die gleiche Strecke zurücklegen würde?
Lösung:
Gesucht ist hier die mittlere Geschwindigkeit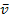 
, also die durchschnittliche Geschwindigkeit des Autos innerhalb der ersten zwei Minuten, d.h. innerhalb der ersten 120 Sekunden. Daher gilt:
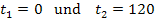
Außerdem ist die Zeit-Geschwindigkeitsfunktion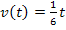 
für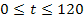 
gegeben. Um die mittlere Geschwindigkeit 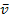zu berechnen, müssen wir nur in die folgende Formel einsetzen:
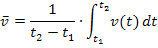
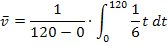
Jetzt rechnen wir das Ganze erst einmal aus;danach werden wir uns dann noch genauer damit beschäftigen, warum das so funktioniert.
Erläuterungen zur Berechnung der mittleren Geschwindigkeit 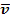innerhalb der ersten 120 Sekunden:
Wie berechnet man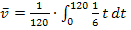 
?
In einem ersten Schritt ermitteln wir eine Stammfunktion zu 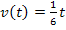. Dazu verwenden wir die Integrationsregel 
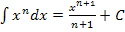. In unserer Aufgabe ist die Variable natürlich t und nicht x;du musst daher die Potenz von t um 1 erhöhen und durch die neue Potenz teilen. Die Zahl 
ist eine multiplikative Konstante, also eine Zahl, mit der multipliziert wird. Solche Zahlen werden beim Integrieren einfach abgeschrieben. Auf „+ C“ kannst du verzichten, weil es sich hier ja um ein bestimmtes Integral handelt, d.h. um ein Integral mit Grenzen. Dabei kann man „+ C“ weglassen.
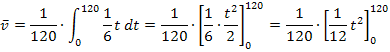
Nun müssen nur noch die Grenzen eingesetzt werden:Obere Grenze minus untere!
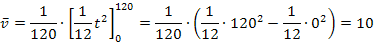
Würde das Auto konstant mit 10 m/s fahren, würde es innerhalb von 120 Sekunden die gleiche Strecke zurücklegen, wie unser Auto, das innerhalb von 120 Sekunden von 0 auf 20 m/s beschleunigt. Die mittlere (durchschnittliche) Geschwindigkeit unseres Autos beträgt somit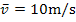 
.
Schauen wir uns das Ganze noch einmal genauer an. Wir haben vorher besprochen, dass die zurückgelegte Strecke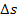 
der Fläche zwischen der Zeit-Geschwindigkeitsfunktion 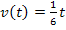und der t-Achse entspricht, also dem bestimmten Integral.
