2. Berechnungen von Mittelwerten mit Hilfe von Integralen
Dann ist die Zeit-Geschwindigkeits-Funktion: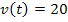 
Der Graph der Zeit-Geschwindigkeits-Funktion ist eine waagrecht verlaufende Gerade. Nun wollen wir die Strecke ermitteln, die das Auto innerhalb der zweiten bis zur zehnten Sekunde ab Versuchsbeginn zurücklegt, also in der Zeitspanne von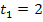 
bis 
.
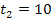Bekanntlich gilt für Bewegungen mit konstanter Geschwindigkeit: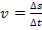 
Wir lösen die Gleichung nach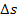 
auf, indem wir mit dem Nenner 
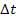multiplizieren.
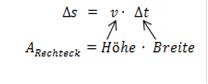
Der zurückgelegte Weg 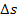entspricht dem Inhalt der rechteckigen Fläche mit der Höhe v und der Breite 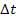. (Wie du weißt, berechnet man den Flächeninhalt eines Rechtecks mit der Formel „Länge der einen Seite mal Länge der anderen Seite“, hier also Höhe v mal Breite 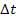.) Dabei gilt außerdem: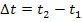 
Betrachte dazu die nachfolgende Abbildung!
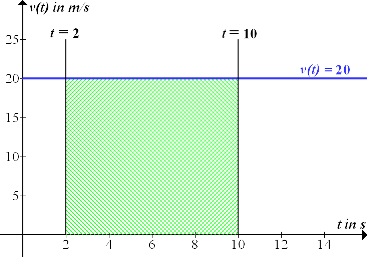
Abb.:Zeit-Geschwindigkeitsfunktion v(t) = 20 mit der Strecke 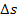, die zwischen der zweiten und zehnten Sekunde zurückgelegt wurde (grün schraffierte Fläche).
Nun können wir leicht die Strecke 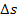berechnen, die zwischen der zweiten und zehnten Sekunde zurückgelegt wurde:
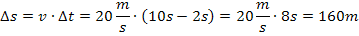
Wenn die gefahrene Geschwindigkeit v konstant ist, ist es also ganz einfach den innerhalb einer bestimmten Zeitspanne zurückgelegten Weg 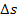zu berechnen.
Nun ist dir hoffentlich klar geworden:Der Weg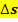 
, der in der Zeitspanne von 
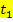bis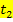 
zurückgelegt wird, entspricht der Fläche zwischen der Zeit-Geschwindigkeitsfunktion 
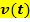und der t-Achse von 
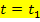(untere Integrationsgrenze) bis 
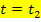(obere Integrationsgrenze).
Allgemein gilt:
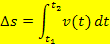
Solange die Geschwindigkeit v konstant ist, ist diese Fläche ein Rechteck und es gilt:
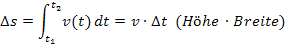
Auf unser Beispiel bezogen, ergibt sich:
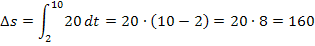
Dasselbe Ergebnis erhält man natürlich auch, wenn man das bestimmte Integral „ganz normal“ ausrechnet, indem man also zuerst eine Stammfunktion ermittelt und dann die Grenzen einsetzt (obere minus untere):
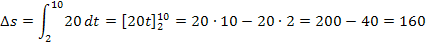
Wenn sich die Geschwindigkeit mit der Zeit ändert, ist die entsprechende Fläche, natürlich kein Rechteck mehr. Um den jeweiligen Flächeninhalt dennoch berechnen zu können, verwenden wir die Integralrechnung. Die zurückgelegte Strecke 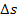benötigen wir, um letztendlich die mittlere (durchschnittliche) Geschwindigkeit 
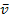zu berechnen, welche ein Körper zwischen 
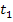und 
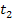hat.
Was ist eigentlich die mittlere Geschwindigkeit 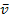? Unter der mittleren Geschwindigkeit 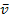versteht man diejenige (konstante) Geschwindigkeit, mit der ein Körper bewegt werden müsste, damit er in der gleichen Zeitspanne 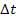die gleiche Strecke 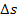zurücklegt, wie der beschleunigte Körper.
