1. Flächenberechnungenmit Hilfe von Integralen
Nullstellen-Berechnung:
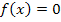
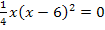
Jetzt nicht ausmultiplizieren! Dadurch würde die Gleichung nicht vereinfacht, sondern verkompliziert werden. Die Gleichung hat nämlich die Form „Produkt = 0“ und ein Produkt ist schließlich genau dann gleich Null, wenn einer der Faktoren gleich Null ist. Wir dürfen daher die Faktoren einzeln gleich Null setzen. Der erste Faktor ist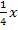 
;er ergibt Null, wenn man für x die Zahl 0 einsetzt. Der zweite Faktor des Produkts ist 
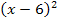;er ergibt Null, wenn man für x die Zahl 6 einsetzt.
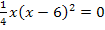
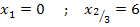
Es gibt also zwei Nullstellen;die kleinere x = 0 entspricht der unteren Grenze des Integrals, das wir berechnen müssen, die größere Nullstelle x = 6 ist entsprechend die obere Grenze.
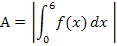
Wir müssen also auf jeden Fall das Integral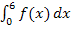 
berechnen. Es bleibt die Frage zu klären, ob wir außerdem den Betrag des Integrals verwenden müssen. Nur wenn die gesuchte Fläche unterhalb der x-Achse liegt, wird das Integral einen negativen Wert ergeben und wir müssen die Betragsstriche um das Integral setzen.
Sicherheitshalber könntest du nun auf jeden Fall den Betrag verwenden;falsch ist er schließlich auch dann nicht, wenn die Fläche oberhalb der x-Achse liegt. Er ist dann bloßnicht zwingend notwendig. Doch kann man sich den Verlauf des Graphen von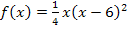 
leicht überlegen. Daher wollen wir das gemeinsam machen.
Bei x = 6 handelt es sich um eine doppelte Nullstelle (siehe auch:Vielfachheiten der Nullstellen), hier schneidet der Graph die x-Achse nicht, sondern berührt sie nur. Bei der einfachen Nullstelle x = 0 wird die x-Achse dagegen von 
wirklich geschnitten. Dieses Wissen hilft beim Skizzieren des Graphen. Wenn man noch einen Kurvenpunkt berechnet, kann man sofort eine aussagekräftige Skizze anfertigen. Man kann zum Beispiel x = 4 nehmen und die zugehörige y-Koordinate ausrechnen. Warum gerade die x-Koordinate x = 4 gewählt wurde? Ganz einfach:Mit x = 4 rechnet es sich hier nämlich ganz leicht, da sich mit 4 kürzen lässt.
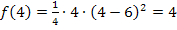
Der Punkt P(4|4) liegt also auf dem Graph . (Dass x- und y-Koordinate des Kurvenpunktes P hier gleich sind, ist reiner Zufall.) Der Punkt P liegt zwischen den beiden Nullstellen, da seine x-Koordinate zwischen den beiden Nullstellen liegt. Weil die y-Koordinate von P positiv ist, weißman, dass im Bereich zwischen den beiden Nullstellen oberhalb der x-Achse verläuft. Da bei der einfachen Nullstelle x = 0 die x-Achse schneidet, liegt hier ein Vorzeichenwechsel von 
vor. Für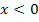 
muss daher unterhalb der x-Achse verlaufen. Bei der doppelten Nullstelle x = 6 liegt dagegen kein Vorzeichenwechsel von vor. Sowohl für 
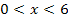als auch für 
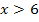muss oberhalb der x-Achse liegen. Betrachte dazu die folgende Abbildung!
