1. Flächenberechnungenmit Hilfe von Integralen
Wir haben bisher nur den Fall behandelt, dass beide Graphen oberhalb der x-Achse verlaufen. Für die Berechnung der Fläche zwischen zwei Funktionen spielt es aber an sich gar keine Rolle, ob die Graphen oberhalb oder unterhalb der x-Achse verlaufen. Die Formel lässt sich nur besonders gut erklären, wenn die Graphen beide oberhalb der x-Achse liegen. Aber auch für den Fall, dass einer der zwei Graphen oder sogar beide unterhalb der x-Achse verlaufen, ließe sich die Gültigkeit der gleichen Formel zeigen. Wir wollen hier jedoch auf die jeweiligen Beweise verzichten.
Merke dir einfach:Bei der Berechnung einer Fläche zwischen zwei Funktionen spielt es keine Rolle, ob die Fläche, die zwischen den beiden Funktionsgraphen liegt, oberhalb der x-Achse, unterhalb oder teils oberhalb und teils unterhalb der x-Achse liegt. (Das ist nur wichtig, wenn die Fläche zwischen einer einzelnen Funktion und der x-Achse berechnet werden soll. Dann braucht man den Betrag des Integrals, wenn die Fläche unterhalb der x-Achse liegt.) Bei der Berechnung der Fläche zwischen zwei Funktionen, brauchst du keinen Betrag, wenn du wirklich die obere Funktion minus die untere rechnest und von der kleineren zur größeren Zahl integrierst.
Was tun, wenn man nicht weiß, welche Funktion im Bereich der Fläche oben und welche unten liegt?
Falls du keine Zeichnung hast und dir die Graphen auch nicht vorstellen kannst, weißt du natürlich nicht, welche Funktion im Bereich der gesuchten Fläche die obere bzw. die untere ist. Dann setzt du einfach um den gesamten Ausdruck einen Betrag, dann kommt auf jeden Fall das richtige Ergebnis heraus.
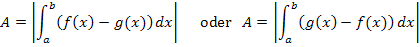
Wenn du Betragsstriche um das Integral setzt, ist es egal, ob du die untere von der oberen Funktion abziehst oder umgekehrt. Dann ist es auch unwichtig, welche Grenze größer oder kleiner ist. Mit dem Betrag gehst du somit auf Nummer sicher.
Aber Vorsicht, egal ob du mit oder ohne Betrag rechnest:Beim Abziehen der einen Funktion von der anderen entweder eine Klammer um die Funktion setzen, die abgezogen werden soll, oder bei dieser Funktion alle Vorzeichen umdrehen! An dieser Stelle passieren erfahrungsgemäßsehr oft Vorzeichenfehler.
· Wenn es drei (oder mehr) Schnittpunkte gibt:
Die drei Schnittpunkte sollen die folgenden x-Koordinaten besitzen:
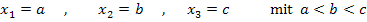
Man integriert zuerst von der kleinsten x-Koordinate a zur nächstgrößeren x-Koordinate b und addiert dazu das Integral von b bis c. Wenn man weiß, welche Funktion das jeweilige Flächenstück oben begrenzt, und welche unten, bildet man jeweils das Integral der oberen minus der unteren Funktion. Dann braucht man keine Beträge. Verlaufen die Graphen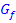 
und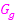 
beispielsweise wie in der folgenden Abbildung gezeigt, dann gilt:
