1. Flächenberechnungenmit Hilfe von Integralen
Wenn du dir den Verlauf des Graphen  einer gegebenen Funktion
einer gegebenen Funktion  nicht vorstellen kannst, weißt du natürlich nicht, welche Flächenstücke oberhalb bzw. unterhalb der x-Achse liegen. Dann setzt du zur Sicherheit einfach um jedes einzelne Integral einen Betrag;dann ist das Ergebnis auf jeden Fall richtig. Du musst den Graph also nicht unbedingt vorher zeichnen, wenn du die Fläche zwischen Graph und x-Achse berechnen sollst. (Besser ist es aber gerade beim Üben, wenn du nicht auf eine Skizze von
nicht vorstellen kannst, weißt du natürlich nicht, welche Flächenstücke oberhalb bzw. unterhalb der x-Achse liegen. Dann setzt du zur Sicherheit einfach um jedes einzelne Integral einen Betrag;dann ist das Ergebnis auf jeden Fall richtig. Du musst den Graph also nicht unbedingt vorher zeichnen, wenn du die Fläche zwischen Graph und x-Achse berechnen sollst. (Besser ist es aber gerade beim Üben, wenn du nicht auf eine Skizze von  verzichtest!)
verzichtest!)
Betrachten wir den Graph  einer Funktion
einer Funktion  mit drei Nullstellen. (Vergleiche dazu die nachfolgende Abbildung!)
mit drei Nullstellen. (Vergleiche dazu die nachfolgende Abbildung!)
Im Folgenden gilt: 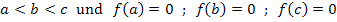
Die drei Nullstellen der Funktion  liegen also bei a, b und c, wobei a die niedrigste Nullstelle ist und c die höchste.
liegen also bei a, b und c, wobei a die niedrigste Nullstelle ist und c die höchste.
Die gesamte Fläche zwischen  und der x-Achse kann dann folgendermaßen berechnet werden:
und der x-Achse kann dann folgendermaßen berechnet werden:
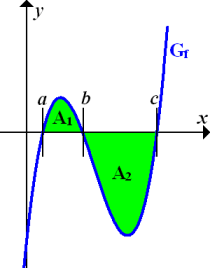 |
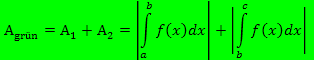 |
Abb.:Bei x = a , x = b und x = c liegen die Nullstellen von  . Der Graph
. Der Graph  einer Funktion
einer Funktion  schließt mit der x-Achse das Flächenstück
schließt mit der x-Achse das Flächenstück 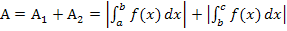 ein. Die Gesamtfläche A setzt sich also aus dem oberhalb der x-Achse liegenden Flächenstück
ein. Die Gesamtfläche A setzt sich also aus dem oberhalb der x-Achse liegenden Flächenstück 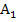 und dem unterhalb der x-Achse liegenden Flächenstück
und dem unterhalb der x-Achse liegenden Flächenstück 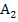 zusammen. (Bei der Berechnung des Inhalts von
zusammen. (Bei der Berechnung des Inhalts von 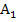 könnte man sich den Betrag sparen, da das zugehörige Integral sowieso positiv ist, nicht aber bei
könnte man sich den Betrag sparen, da das zugehörige Integral sowieso positiv ist, nicht aber bei 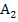 .)
.)
Die Fläche zwischen  und der x-Achse von a bis b liegt oberhalb der x-Achse. Daher kann beim Integral von a bis b zwar ein Betrag gesetzt werden, muss es aber nicht. Dagegen liegt die Fläche zwischen
und der x-Achse von a bis b liegt oberhalb der x-Achse. Daher kann beim Integral von a bis b zwar ein Betrag gesetzt werden, muss es aber nicht. Dagegen liegt die Fläche zwischen  und der x-Achse von b bis c unterhalb der x-Achse. Beim Integral von b bis c muss daher unbedingt der Betrag verwendet werden, wenn man die Fläche berechnen will.
und der x-Achse von b bis c unterhalb der x-Achse. Beim Integral von b bis c muss daher unbedingt der Betrag verwendet werden, wenn man die Fläche berechnen will.
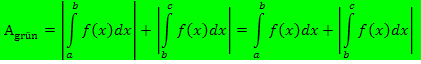
Fassen wir noch einmal das Wichtigste kurz zusammen.
Fläche berechnen, die 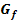 mit der x-Achse einschließt mit der x-Achse einschließt
Anleitung:
(Bei den Flächenstücken, die oberhalb der x-Achse liegen, kann auf den Betrag gegebenenfalls verzichtet werden. Bei den Flächenstücken, die unterhalb der x-Achse liegen, ist der Betrag zwingend notwendig.) |
1.2 Fläche zwischen zwei Funktionen
Gegeben sind zwei Funktionen  und
und 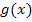 . Gesucht ist die Fläche, die von diesen beiden Funktionen eingeschlossen wird.
. Gesucht ist die Fläche, die von diesen beiden Funktionen eingeschlossen wird.
1. Schritt:Grenzen berechnen
Zuerst muss man die x-Koordinaten, die sogenannten Abszissen, der Schnittpunkte herausfinden;das sind nämlich die Integrationsgrenzen. Du musst also zuerst die beiden Funktionen gleichsetzen und die entstehende Gleichung nach x auflösen.

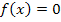
 Grenzen
Grenzen