1. Flächenberechnungenmit Hilfe von Integralen

Jetzt fehlt nur noch 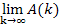. Diesen Grenzwert müssen wir noch berechnen. Das bedeutet, dass wir die obere Grenze k des Integrals 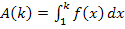unendlich großmachen sollen, also dass die senkrechte Gerade x = k extrem weit nach rechts verschoben werden soll. Wir müssen demnach eigentlich 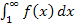berechnen, was anschaulich der Fläche entspricht, die ab x = 1 zwischen und der x-Achse liegt. (In der nächsten Abbildung ist die entsprechende Fläche zu sehen.) Diese Fläche erstreckt sich im I. Quadranten ins Unendliche, da die x-Achse die waagrechte Asymptote von ist. Ob diese Fläche unendlich großwird oder einen endlichen Flächeninhalt hat, das sollen wir nun herausfinden. Wir müssen dazu den Grenzwert 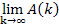bilden, d.h. k bei 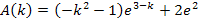gegen Unendlich gehen lassen.

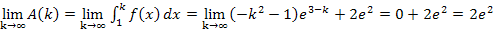
Die Fläche ist also nicht unendlich groß, obwohl sie sich ins Unendliche erstreckt. Ihr Inhalt wird nicht größer als .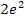

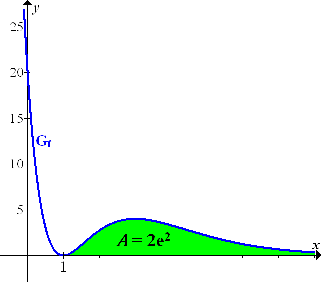
Dir ist nicht klar, wie man auf das Ergebnis 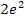gekommen ist? Ok, dann noch einmal aber ganz langsam mit einigen Zwischenschritten, die man normalerweise nicht aufschreibt. Streng genommen sind die folgenden Schritte reine Überlegungen im Kopf. (Also bitte in Prüfungen nicht auf das Papier schreiben!)

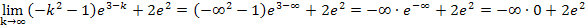
Nun stehen wir vor dem Problem, dass 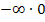ein unbestimmter Ausdruck ist, dass man also nicht generell sagen kann, was dabei herauskommt. Bekanntlich setzt sich allerdings immer derjenige Ausdruck bzw. die Zahl durch, die von der e-Funktion kommt. In diesem Fall kommt die Zahl 0 von der e-Funktion. Die Zahl 0 setzt sich hier gegenüber dem Unendlich durch. Deshalb gilt in diesem Fall: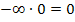

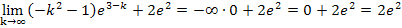
Mehr zu Integralen, die Unendlich als Grenze aufweisen, findest du im gesonderten Teil Uneigentliche Integrale.

Nun haben wir verschiedene Beispiele zur Flächenberechnung mit Hilfe von Integralen besprochen. Man kann mit Integralen aber nicht nur Flächen berechnen, sondern auch Mittelwerte. Wie das funktioniert, wird im gesonderten Teil 2. Berechnungen von Mittelwerten mit Hilfe von Integralenbesprochen.

---