1. Flächenberechnungenmit Hilfe von Integralen
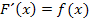
Daher muss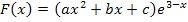 
erst einmal abgeleitet werden, damit nachher die Parameter a, b und c bestimmt werden können. Um F abzuleiten, benutzen wir die Produktregel. (Es handelt sich bei F schließlich um ein Produkt, das in beiden Faktoren die Variable x enthält. Die Parameter a, b und c müssen beim Ableiten als Konstanten angesehen werden, also als feste Zahlen, nicht als Variablen.) Beim Ableiten des zweiten Faktors muss außerdem laut Kettenregel nachdifferenziert, d.h. mit der Ableitung der inneren Funktion multipliziert werden. Daher kommt die Zahl -1 am Ende der folgenden Zeile.
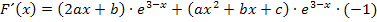
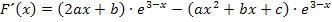
Wir klammern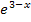 
aus. Das ergibt:
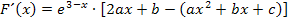
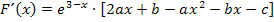
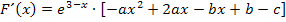
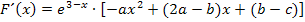
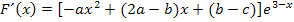
Wegen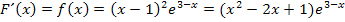 
gilt:
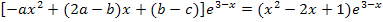
Mit Hilfe eines Koeffizientenvergleichs können wir jetzt drei Gleichungen für die drei Unbekannten a, b und c aufstellen.
Der Ausdruck und diejenige Zahl, die auf der linken bzw. auf der rechten Seite der Gleichung vor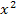 
stehen, müssen gleich sein. (Unten in Lila geschrieben.) Das führt zur Gleichung I.
Entsprechend sind der Ausdruck und diejenige Zahl gleich, die auf der linken bzw. auf der rechten Seite der Gleichung vor x stehen. (Unten in Rosa geschrieben.) Das liefert Gleichung II.
Ebenso müssen der Ausdruck ohne x auf der linken Seite der Gleichung und diejenige Zahl ohne x, die auf der rechten Seite der Gleichung steht, gleich sein. (Unten in Blau geschrieben.) Das ergibt Gleichung III.
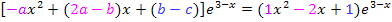
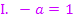
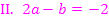
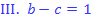
Aus I. folgt:
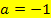
a in II. eingesetzt:
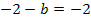
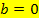
b in III. eingesetzt:
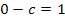
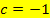
Nun können wir die ermittelten Werte für a, b, und c in 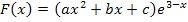einsetzen.
Die gesuchte Stammfunktion zu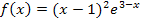 
ist somit 
.
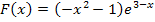Zu 12f.)
Es soll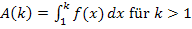 
berechnet werden. Dazu brauchst du die in Teilaufgabe 12e.) ermittelte Stammfunktion 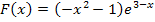, da du 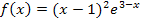selbst nicht integrieren kannst.
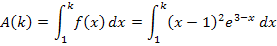
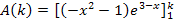
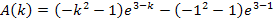
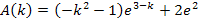
Was haben wir da eigentlich berechnet? Da der Graph der Funktion 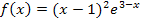nicht unterhalb der x-Achse verläuft, entspricht das Integral 
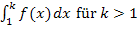der Fläche zwischen dem Graph 
, der x-Achse von x = 1 bis x = k. Die Gerade x = 1 verläuft parallel zur y-Achse im Abstand 1;sie begrenzt die Fläche auf der linken Seite. Auch die Gerade x = k verläuft parallel zur y-Achse;wegen k >1 liegt die Gerade x = k rechts von der senkrechten Gerade x = 1. Somit begrenzt die senkrechte Gerade x = k die Fläche auf der rechten Seite. Damit du dir das Ganze besser vorstellen kannst, wählen wir einen konkreten Zahlenwert für k (zum Beispiel k = 6) und tragen die beiden senkrechten Geraden in die Zeichnung mit ein. Außerdem markieren wir die entsprechende Fläche A(k) grün. Siehe folgende Abbildung!
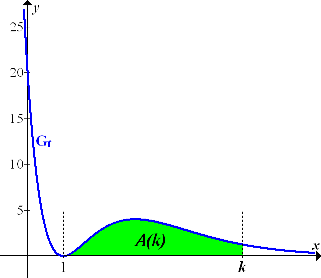
Abb.:Graph der Funktion 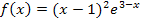mit der Fläche 
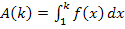mit k = 6
