1. Flächenberechnungenmit Hilfe von Integralen

Ist die zweite Ableitung an der entsprechenden Stelle positiv, ist der Graph dort linksgekrümmt und es liegt ein Tiefpunkt vor.

Ist die zweite Ableitung an der jeweiligen Stelle dagegen negativ, handelt es sich um einen Hochpunkt, da der Graph dann rechtsgekrümmt ist.

(Wenn Null herauskommt, liegt kein Extremum vor, sondern mit größter Wahrscheinlichkeit ein Terrassenpunkt. Das müsste dann jedoch bei den Wendepunkten noch nachgewiesen werden. Ein Terrassenpunkt ist schließlich ein Wendepunkt mit waagrechter Tangente.)

An sich ist diese Methode ganz einfach, aber bei dieser Aufgabe dauert es ziemlich lange bis man die zweite Ableitung gebildet hat. Man benötigt dazu wieder die Produkt- und Kettenregel. Nur wenn du Probleme mit der Monotonieuntersuchung hast, solltest du bei dieser Aufgabe die Art der Extrema mit Hilfe der zweiten Ableitung ermitteln.

Hier noch einmal die erste Ableitung: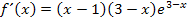

Um die zweite Ableitung zu berechnen, multiplizieren wir vorweg die Klammern in der ersten Ableitung aus, damit wir nachher ein Produkt vorliegen haben, das nur zwei Faktoren hat, die jeweils x enthalten. (Wir haben nämlich keine Produktregel für Produkte mit drei Faktoren, die jeweils x enthalten. Die Produktregel ist schließlich nur auf Produkte anwendbar, die in genau zwei Faktoren die Variable x enthalten.)

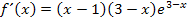
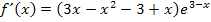
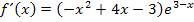
Berechnung der zweiten Ableitung nach der Produktregel (und Kettenregel):

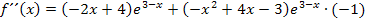
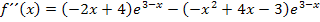
Wir klammern den Faktor 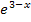aus. Das ergibt:

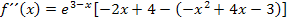
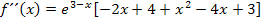
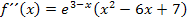
Weiter lässt sich die zweite Ableitung nicht vereinfachen. Als nächstes werden jeweils die oben berechneten x-Koordinaten x = 1 und x = 3 in die zweite Ableitung eingesetzt.

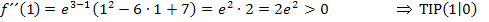
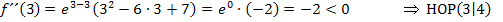
Zu 12d.)

Hier noch einmal die Funktionsgleichung: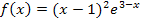

Es sollen näherungsweise die Funktionswerte f (0,2) und f (9) berechnet werden, d.h. die zugehörigen y-Koordinaten zu x = 0,2 und x = 9.

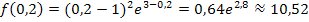
Zusammenfassung der wichtigsten Ergebnisse der Teilaufgaben 12a.) bis 12d):

Für 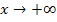waagrechte Asymptote:y = 0 (x-Achse)

Doppelte Nullstelle / Tiefpunkt TIP (1|0)

Hochpunkt HOP (3|4)

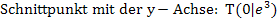
Bekannte Kurvenpunkte:(0,2|10,52)  (9|0,16)

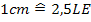Mit Hilfe der bisherigen Ergebnisse kann der Graph nun in einem Koordinatensystem skizziert werden. Für die y-Achse empfiehlt sich beispielsweise ein Maßstab von , da die y-Werte teilweise sehr hoch sind. Für die x-Achse kann ein Maßstab von 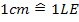gewählt werden.

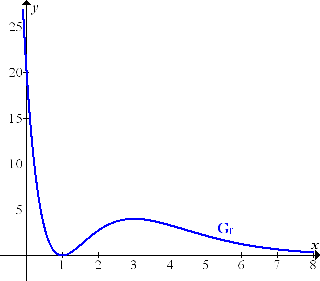
Abb.:Graph der Funktion

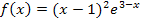
Zu 12e.)

Es sollen die Parameter a, b und c bestimmt werden, so dass 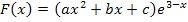eine Stammfunktion zu 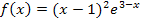ist.

Bekanntlich gilt für eine Stammfunktion F zu einer Funktion f der folgende Zusammenhang:

---