1. Flächenberechnungenmit Hilfe von Integralen

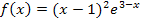
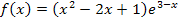
Berechnung der ersten Ableitung nach der Produktregel (und Kettenregel):

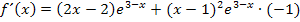
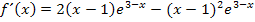
Nun klammern wir 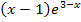aus. Das ergibt:

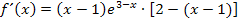
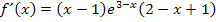
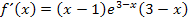
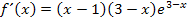
Hinweis:Hätten wir vorher nicht 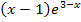ausgeklammert, sondern die Klammern ausmultipliziert, hätten wir an Stelle der beiden vorderen Klammern 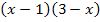den Ausdruck 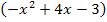erhalten. Falls du die Aufgabe selbst gerechnet hast und dabei auf die Ableitung 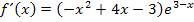gekommen bist, hast du nichts falsch gemacht. Auch 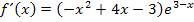ist richtig, aber die andere Form der Ableitung ist praktischer, da sie sich leichter gleich Null setzen lässt.

Du weißt:Ein Produkt ist gleich Null, wenn einer der Faktoren gleich Null ist. Daher darf man die Faktoren eines Produkts auch einzeln gleich Null setzen.

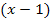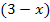Auf unsere Aufgabe bezogen bedeutet das, dass wir einfach die Klammern und jeweils einzeln gleich Null setzen können. Der Faktor 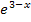ist immer positiv;er kann gar nicht gleich Null werden, egal was für x eingesetzt wird. Wir können diesen Faktor ignorieren.

Willst du dagegen mit 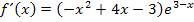rechnen, kannst du ebenfalls den Faktor 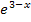ignorieren, da er, wie gesagt, nicht gleich Null werden kann. Du musst ausschließlich die Klammer 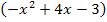gleich Null setzen. Die entstehende gemischtquadratische Gleichung lässt sich mit der Mitternachtsformel lösen, doch ist das umständlicher.

Wir verwenden hier lieber die Ableitung in der Form .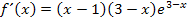

Berechnung der Extrema:

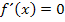
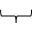
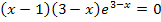
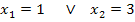
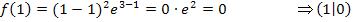
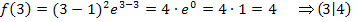
Art der Extrema untersuchen:

Um herauszufinden, ob es sich dabei jeweils um einen Hochpunkt oder Tiefpunkt handelt oder bloßum einen Terrassenpunkt, d.h. gar kein Extremum, gibt es zwei Möglichkeiten.

1. Methode:Untersuchung des Monotonieverhaltens

Wir müssen das Vorzeichen der ersten Ableitung ermitteln. Die Funktion ist für alle reellen Zahlen definiert;es gibt also keine Definitionslücken, die wir in die Monotonietabelle aufnehmen müssen. Nur bei x = 1 und x = 3 kann sich die Monotonie, d.h. das Steigungsverhalten ändern.

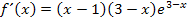
x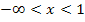
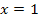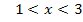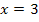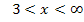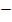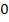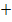	fällt	TIP	steigt	HOP	fällt

Das Vorzeichen der ersten Ableitung ändert sich sowohl an der Stelle x = 1 als auch bei x = 3. Daher handelt es sich bei den Punkten (1|0) und (3|4) jeweils um einen Extrempunkt und nicht um einen Terrassenpunkt. An Hand des Steigungsverhaltens von , vergleiche Pfeile in der Tabelle, wird klar, dass bei x = 1 ein relativer Tiefpunkt und bei x = 3 ein relativer Hochpunkt vorliegt.

2. Methode:Mit der zweiten Ableitung

Diese Methode ist hier nicht zu empfehlen, da sie in diesem Fall wesentlich länger dauert. Man muss dazu nämlich die zweite Ableitung berechnen und die x-Koordinaten der oben berechneten Punkte mit waagrechter Tangente x = 1 und x = 3 in die zweite Ableitung einsetzen. Am Vorzeichen des jeweiligen Ergebnisses kann man dann ablesen, was für ein Extremum vorliegt.

---