1. Flächenberechnungenmit Hilfe von Integralen

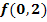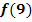d.) Berechne näherungsweise die Funktionswerte und . Zeichne dann mit Hilfe der bisherigen Ergebnisse den Graphen 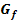in ein Koordinatensystem.

e.) Wie müssen die Parameter a ℝ, b ℝ und c ℝ gewählt werden, dass eine Stammfunktion von 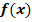ist?

f.) Berechne für k >1 in Abhängigkeit von k :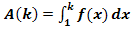

Ermittle sodann 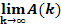und interpretiere das Ergebnis geometrisch-anschaulich!

Lösung:

Zu 12a.)

Gegeben ist die Funktion 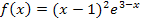mit ihrer maximalen Definitionsmenge 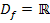. Gesucht sind die Nullstelle und der Schnittpunkt T mit der y-Achse.

Berechnung der Nullstelle bzw. des Schnittpunkts mit der x-Achse:

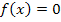
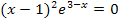
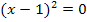
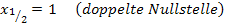
Erläuterung:Ein Produkt ist gleich Null, wen ein Faktor Null ist. Daher dürfen die Faktoren des Produkts einzeln gleich Null gesetzt werden. Da der Faktor 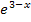immer positiv ist, kann er nicht gleich Null werden. Wir können diesen Faktor ignorieren. Wir müssen daher nur den Faktor 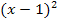gleich Null setzen. Die Lösung x = 1 lässt sich dann sofort ablesen, denn nur für x = 1 ergibt die Klammer (x – 1)  Null und somit auch das Quadrat davon. Es handelt sich bei x = 1 um eine doppelte Nullstelle, was man an dem Quadrat außerhalb der Klammer erkennt. Der Graph schneidet bei x = 1 die x-Achse also nicht, sondern berührt sie nur. (Siehe auch:Vielfachheiten der Nullstellen) Bei N(1|0) muss demnach ein Extremum von sein.

Berechnung des Schnittpunkts mit der y-Achse:

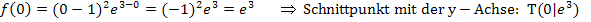
Zu 12b.)

Verhalten im Unendlichen:

Die Definitionsmenge ist 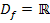. Es müssen daher die Grenzwerte 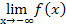und 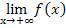berechnet werden.

Zur Erinnerung: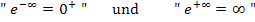

Vorsicht bei unbestimmten Ausdrücken, d.h. Ausdrücke der Form:

Dabei kann man nicht generell sagen, was heraus kommt! Das Ergebnis hängt bei 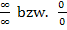davon ab, welches 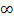bzw. welche 0 sich durchsetzt, also von welcher Funktion das jeweilige 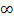bzw. die Null kommt.

Grundsätzlich gilt:

Die e-Funktion wächst schneller als jedes Polynom oder eine ln-Funktion. Das Unendlich, das von der e-Funktion kommt, bzw. die Null, welche von der e-Funktion kommt, ist stärker.

Beim Verhalten für ergibt sich in diesem Fall kein unbestimmter Ausdruck, jedoch aber für .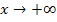

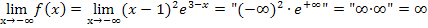
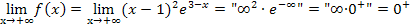
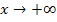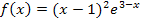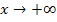Für hat eine waagrechte Asymptote. Sie hat die Gleichung y = 0;es handelt sich daher um die x-Achse. Der Graph nähert sich für von oben an die x-Achse an. (Das erkennt man an dem Vorzeichen der Null. Das Plus-Zeichen bei 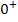deutet an, dass sich die Funktion von oben an die waagrechte Asymptote annähert.)

Zu 12 c.)

Um die Extrema der Funktion 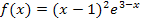zu berechnen, benötigen wir die erste Ableitung. Da es sich bei um ein Produkt handelt, das in beiden Faktoren die Variable x enthält, müssen wir die Produktregel anwenden. Um den ersten Faktor 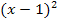abzuleiten, kann entweder vorweg die zweite binomische Formelzur Vereinfachung benutzt und dann mit der Ableitungsregel 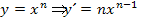abgeleitet werden oder (ohne die Klammer vorher zu quadrieren) direkt mit der Kettenregelgearbeitet werden. Man müsste dann mit der Zahl 1 nachdifferenzieren, was man sich natürlich schenken kann. Wir vereinfachen im Folgenden den ersten Faktor mit Hilfe der binomischen Formel, da die meisten Schüler vermutlich diese Methode bevorzugen. Den zweiten Faktor 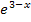können wir nur mit der Kettenregel ableiten;da gibt es keine andere Möglichkeit. Die äußere Funktion ist die e-Funktion, die innere Funktion 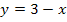. Die Ableitung der inneren Funktion ist -1. Daher dürfen wir nicht vergessen mit -1 nachzudifferenzieren (d.h. noch mit -1 zu multiplizieren), wenn wir den zweiten Faktor ableiten.

---