1. Flächenberechnungenmit Hilfe von Integralen

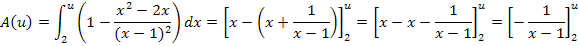
Als nächstes werden die Grenzen eingesetzt:Obere minus untere

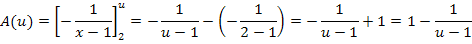
Nun haben wir die gesuchte Fläche in Abhängigkeit von u ermittelt:

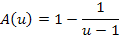
Als letztes muss noch 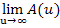berechnet und geometrisch-anschaulich interpretiert werden.

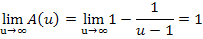
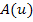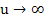Nicht klar? Also dann noch einmal ganz langsam:Wenn u unendlich großwird, dann wird der Nenner des Bruchs ebenfalls unendlich groß;dadurch wird der Bruch insgesamt sehr, sehr klein. Der Bruch geht dann also gegen Null;er wird vernachlässigbar klein. Daher geht für gegen 1.

Lässt man bei 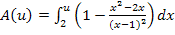die obere Grenze u gegen Unendlich sterben, bedeutet dies anschaulich, dass wir die senkrechte Gerade x = u unendlich weit nach rechts verschieben, d.h. wir wollen eigentlich wissen, wie großdas Integral 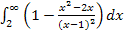wird.

Geometrisch-anschaulich bedeutet dies, dass die Fläche zwischen 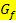, der waagrechten Asymptoten und der senkrechten Geraden x = 2, welche sich im I. Quadranten ins Unendliche erstreckt, nicht größer als 1 werden kann.

Das Besondere daran ist, dass sich die Fläche zwar ins Unendliche erstreckt, ihr Flächeninhalt jedoch trotzdem beschränkt ist also nicht unendlich groß wird. Man kann sich das nur so erklären, dass zwar immer noch etwas dazu kommt zu der Fläche, wenn man die obere Grenze noch größer macht, dass aber die Flächenzuwächse immer kleiner werden und irgendwann nicht mehr ins Gewicht fallen. Der Inhalt der Fläche zwischen der Funktion und ihrer waagrechten Asymptote, die linksseitig durch die senkrechte Gerade x = 2 begrenzt wird, die sich jedoch nach rechts ins Unendliche erstreckt, nähert sich an die Zahl 1 an – exakt den Wert 1 wird diese Fläche aber niemals annehmen. Ausführlicher wird diese Thematik im Teil Uneigentliche Integrale erklärt. Das ist aber nicht bei allen Flächen, die sich ins Unendliche erstrecken, so. Manche haben einen endlichen Inhalt, andere werden allerdings tatsächlich unendlich groß. Das hängt von der jeweiligen Funktion und Fläche ab.

Auch im folgenden Beispiel geht es um eine Fläche, die sich ins Unendliche erstreckt.

12. Bsp.:Fläche zwischen dem Graph einer e-Funktion und ihrer waagrechten Asymptoten – Noch einmal eine Fläche, die sich zwar ins Unendliche erstreckt, die aber einen endlichen Wert besitzt

Gegeben ist die Funktion 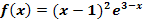mit ihrer maximalen Definitionsmenge 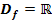. Ihr Graph wird mit 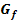bezeichnet.

a.) Bestimme die Nullstelle von 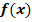und den Schnittpunkt T von 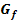mit der y-Achse.

b.) Untersuche das Verhalten von 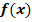im Unendlichen und gib die Gleichung der Asymptote vo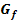n an!

c.) Bestimme Art und Lage der Extrempunkte von .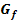

---