1. Flächenberechnungenmit Hilfe von Integralen
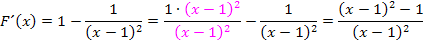
Mit Hilfe der zweiten binomischen Formellösen wir die Klammer im Zähler auf.
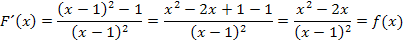
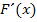stimmt mit 
überein. Genau das sollte gezeigt werden. Daher ist 
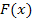eine Stammfunktion zu .
Du möchtest auch noch die andere Variante sehen, wobei man zuerst bei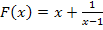 
alles auf einen gemeinsamen Bruchstrich schreibt und erst danach die Quotientenregel zum Ableiten anwendet? Dann gehe zu:Ableitung nach Variante 2 zu Bsp. 11e.)
Zu 11f.)
Es soll der Inhalt der Fläche zwischen dem Graph 
der Funktion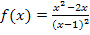 
, ihrer waagrechten Asymptoten, also der Gerade y = 1, sowie den senkrechten Geraden x = 2 und x = u mit u >2 in Abhängigkeit von u berechnet werden.
In Teilaufgabe 11d.) haben wir den Graph der Funktion 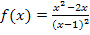samt ihrer waagrechten Asymptote y = 1 schon gezeichnet. In dasselbe Koordinatensystem zeichnen wir nun auch die senkrechte Gerade x = 2 und als Beispiel für die senkrechte Gerade x = u mit u >2 die konkrete Gerade x = 5. (Die Zahl 5 ist ein willkürlich gewähltes Beispiel. Du hättest natürlich auch an Stelle der Zahl 5 irgendeine andere Zahl über 2 nehmen und die entsprechende Gerade einzeichnen können. Wir verwenden einfach irgendein konkretes Beispiel für x = u mit u >2, damit du dir das Ganze besser vorstellen kannst. Eigentlich beschreibt die Gleichung x = u mit u >2 eine Schar von senkrechten Geraden, wobei jede der Geraden wegen u >2 rechts von der senkrechten Gerade x = 2 liegt.) Außerdem schraffieren wir die gesuchte Fläche farbig. Vergleiche dazu die folgende Abbildung!
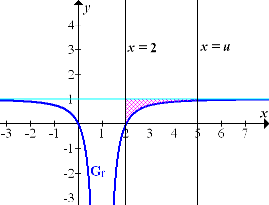
Abb.:Graph 
der Funktion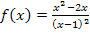 
mit der waagrechten Asymptoten y = 1 und den senkrechten Geraden x = 2 und x = u (mit u = 5)
Nun berechnen wir die gesuchte Fläche in Abhängigkeit von u, d.h. wir dürfen jetzt natürlich nichts Konkretes mehr für u einsetzen. Wir rechnen einfach so, als wäre u eine feste Zahl größer 2. Da wir eine Fläche zwischen zwei Funktionen suchen, nämlich die Fläche zwischen der Funktion und ihrer waagrechten Asymptote y = 1, müssen wir das Integral der oberen minus der unteren Funktion berechnen. Weil die waagrechte Asymptote oberhalb liegt, muss von der Asymptotengleichung y = 1 die Funktionsgleichung 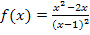abgezogen und davon das Integral von 2 bis u berechnet werden. Wegen u >2 ist u die obere Grenze.
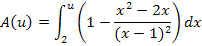
Um das Integral zu berechnen, brauchen wir eine Stammfunktion. Die Zahl 1 ergibt integriert x, den Bruch brauchen wir nicht selbst zu integrieren, da wir in Teilaufgabe 11e.) schon nachgewiesen haben, dass 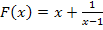eine Stammfunktion von 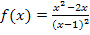ist. Somit wissen wir, dass 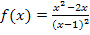integriert 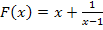ergibt.
