1. Flächenberechnungenmit Hilfe von Integralen
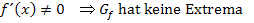
Das heißt aber nicht, dass die Funktion ihr Steigungsverhalten nicht ändern kann. An der Definitionslücke x = 1 ändert sich das Vorzeichen der Ableitung. Es handelt sich dabei nämlich um einen Pol ohne Vorzeichenwechsel (vergleiche Teilaufgabe 11b.) und bei Polen ohne Vorzeichenwechsel ändert sich grundsätzlich das Monotonieverhalten. Das erkennt man natürlich auch an der Ableitung. Wegen der ungeraden Potenz im Nenner ändert sich das Vorzeichen von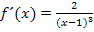 
an der Stelle x = 1.
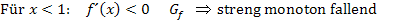
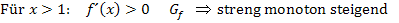
Zu 11d.)
Mit Hilfe der bisherigen Ergebnisse lässt sich der Graph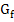 
gut skizzieren. Zuerst die Nullstellen bei x = 0 und x = 2 sowie die senkrechte Asymptote x = 1 und die waagrechte Asymptote y = 1 in ein Koordinatensystem mit 
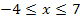eintragen. In der Umgebung der senkrechten Asymptote muss der Graph 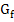auf beiden Seiten 
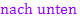schießen, wegen 
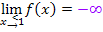und 
.
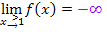In der folgenden Abbildung kannst du den Graph mit seinen Asymptoten sehen.
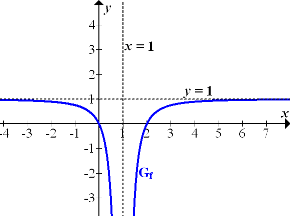
Abb.:Graph der Funktion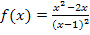 
mit Asymptoten (gestrichelt)
Zu 11e.)
Es soll gezeigt werden, dass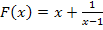 
eine Stammfunktion von 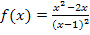ist. Wie macht man das?
Du weißt hoffentlich:Es ist zu beweisen, dass Folgendes gilt:
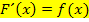
Daher leiten wir die angegebene Stammfunktion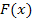 
ab und formen das Ergebnis so lange um, bis es mit 
übereinstimmt. Das muss klappen, denn laut Angabe ist 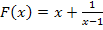eine Stammfunktion zu 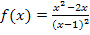. Wenn sich 
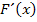nicht so umformen lässt, dass wieder herauskommt, dann hast du dich verrechnet oder 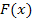ist gar keine Stammfunktion von , was hier jedoch nicht sein kann!
Hinweise zum Ableiten von :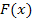
Um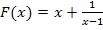 
abzuleiten, verwenden wir unteranderem die Quotientenregel. Man könnte vor dem Ableiten entweder alles auf einen gemeinsamen Bruchstrich schreiben, indem man bei x mit (x – 1) erweitert, oder man leitet sofort ab, ohne vorher alles zu einem gemeinsamen Bruch zusammenzufassen. Wir wählen hier die letztere Variante.
Es handelt sich bei 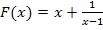um eine Summe mit x als ersten Summanden und dem Bruch als zweiten Summanden. Bei Summen darf man bekanntlich einfach jeden Summanden einzeln ableiten. Wir können daher x und den Bruch getrennt ableiten. x abgeleitet ergibt die Zahl 1. Um den Bruch abzuleiten, verwenden wir die Quotientenregel.
Vorsicht beim Ableiten des Zählers:Die Zahl 1 ergibt abgeleitet 0;diese Null darf man bei der Quotientenregel nicht einfach weglassen!
Bilde nun selbst die Ableitung von 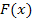, bevor du dir den Rest der Lösung anschaust!
Zu Zeigen: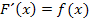 
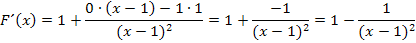
Jetzt bringen wir alles auf einen gemeinsamen Nenner;d.h. wir erweitern bei der Zahl 1 mit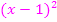 
. Dann können wir alles auf einen gemeinsamen Bruchstrich schreiben.
