1. Flächenberechnungenmit Hilfe von Integralen

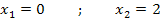
Der Graph schneidet die x-Achse in den Punkten 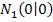und .

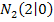2. Schnittpunkt mit der y-Achse

Um den Schnittpunkt einer Funktion mit der y-Achse zu berechnen, muss in die Funktionsgleichung für x die Zahl 0 eingesetzt werden. Jeder Punkt der y-Achse hat schließlich die x-Koordinate x = 0. Es muss somit berechnet werden.

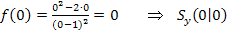
Wir hätten uns hier die Arbeit sparen können. Da eine der Nullstellen bei x = 0 liegt, war es sowieso klar, dass der Graph die y-Achse im Ursprung schneidet.

Zu 11b.)

Es soll das Verhalten von 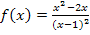an den Rändern des Definitionsbereichs untersucht und die Gleichungen aller Asymptoten angegeben werden. Das bedeutet, dass das Verhalten im Unendlichen und an der Definitionslücke x = 1 links- und rechtsseitig untersucht werden soll. Dazu müssen wir die folgenden Grenzwerte berechnen:

Verhalten im Unendlichen:

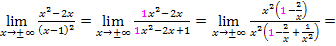
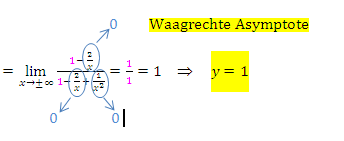
Verhalten in der Umgebung der Definitionslücke:

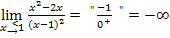
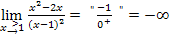
Es liegt ein Pol ohne Vorzeichenwechsel vor, was auch an der geraden Potenz der Klammer im Nenner erkennbar ist. (Ein Pol zweiter Ordnung/ gerader Ordnung ist immer ohne Vorzeichenwechsel.) Die Funktion hat bei x = 1 eine senkrechte Asymptote.

Zu 11c.)

Es soll das Monotonieverhalten (Steigungsverhalten) der Funktion 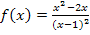untersucht und damit gezeigt werden, dass kein Extremum existiert. Die erste Ableitung entspricht bekanntlich der Tangentensteigung der Funktion . Damit es kein Extremum gibt, darf die Ableitung nicht gleich Null werden. Genau dies gilt es zu zeigen.

Wir leiten 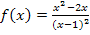mit Hilfe der Quotientenregel ab, da die Variable x im Nenner des Bruchs vorkommt. Bei der Quotientenregel muss unteranderem die Ableitung des Nenners gebildet werden. Um den Nenner abzuleiten, kannst du entweder vorher die Klammer mit der zweiten binomischen Formelquadrieren und den ausgerechneten Nenner „ganz normal“ ableiten oder du lässt die Klammer mit dem Quadrat bei einfach stehen und leitest den Nenner mit der Kettenregel ab. Wir werden hier die zuletzt genannte Methode mit der Kettenregel verwenden, da sich die Ableitung dann besser vereinfachen lässt. (Man erkennt dann nämlich leichter, dass sich im Zähler von der Faktor (x – 1) ausklammern lässt. Danach kann man mit genau diesem Faktor kürzen. So wird wesentlich vereinfacht.) Genauere Erklärungen zur Anwendung von Quotienten- und Kettenregel findest bei:Weitere Ableitungsregeln

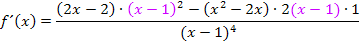
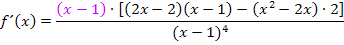
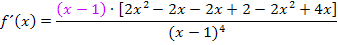
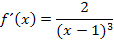
Die Ableitung kann niemals gleich Null sein, denn ein Bruch ergibt nur dann Null, wenn der Zähler Null ist. Der Zähler von enthält jedoch gar kein x und kann somit nicht gleich Null sein. Daher gibt es keine Extrema.

---