1. Flächenberechnungenmit Hilfe von Integralen
Wir müssen daher stückweise integrieren:Bei der Nullstelle bzw. den Nullstellen von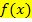 
muss das Integral geteilt werden. Um die einzelnen Integrale wird dann jeweils ein Betragsstrich gesetzt;zum Schluss werden die Ergebnisse alle addiert. Das ergibt dann die gesuchte Gesamtfläche.
Anmerkung:Eigentlich musst du nur um diejenigen Integrale einen Betrag setzen, die negative Ergebnisse liefern würden, also nur bei den Flächenstücken, die unterhalb der x-Achse liegen. Bei den anderen kann man sich den Betrag an sich sparen, er schadet aber auch nicht.
Gehen wir beispielsweise davon aus, dass die Funktion 
im Intervall von a bis b die Nullstelle c besitzt 
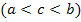und dass 
den Verlauf hat wie in der folgenden Abbildung. Dann lässt sich der Gesamtflächeninhalt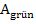 
auf jeden Fall berechnen durch:
 |
 |
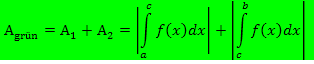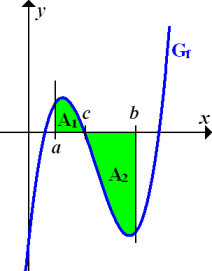
Abb.:Der Graph einer Funktion schließt mit der x-Achse und den Geraden x = a und x = b das Flächenstück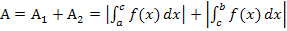 
ein. Es setzt sich aus dem oberhalb der x-Achse liegenden Flächenstück 
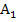und dem unterhalb der x-Achse liegenden Flächenstück 
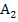zusammen. (Bei der Berechnung des Inhalts von 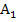könnte man sich den Betrag sparen, da das zugehörige Integral sowieso positiv ist, nicht aber bei .)
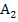Die Fläche zwischen und der x-Achse von a bis c liegt oberhalb der x-Achse. Beim Integral von a bis c muss daher nicht unbedingt ein Betrag gesetzt werden. Dagegen liegt die Fläche zwischen und der x-Achse von c bis b unterhalb der x-Achse. Beim Integral von c bis b muss daher ein Betrag gesetzt werden, wenn man die Fläche berechnen will.
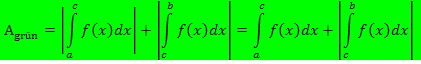
2. Typ: Berechnung der Fläche, welche von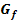 
und der x-Achse eingeschlossen wird
Es sind also keine Grenzen gegeben, nur die Gleichung der Funktion . Die Integrationsgrenzen entsprechen dann den Nullstellen der Funktion . Man integriert dann von der kleinsten (ersten) Nullstelle zur nächst größeren (zweiten) Nullstelle und setzt Betragsstriche um das Integral. Zum Betrag des ersten Integrals addiert man dann den Betrag des Integrals von der zweiten Nullstelle zur nächst größeren (dritten) Nullstelle. Falls noch mehr Nullstellen existieren, addiert man außerdem den Betrag des Integrals von der dritten bis zur vierten Nullstelle usw.
Kurz gesagt, man integriert von Nullstelle zu Nullstelle, von der niedrigsten zur nächsthöheren usw., quasi von links nach rechts. Um jedes einzelne Integral wird zur Sicherheit ein Betrag gesetzt und alles addiert. Der Betrag um das Integral ist eigentlich nur dann nötig, wenn das entsprechende Flächenstück unterhalb der x-Achse liegt. Liegt das Flächenstück oberhalb der x-Achse, kann auf den Betrag verzichtet werden.
