1. Flächenberechnungenmit Hilfe von Integralen

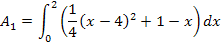
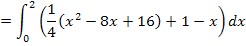
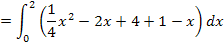
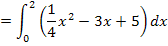
Nun können wir das Integral leicht berechnen. Um eine Stammfunktion zu finden verwenden wir die Regel .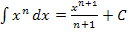

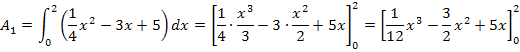
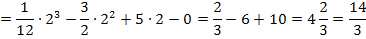
Die gesamte gesuchte Fläche 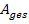ist doppelt so großwie .

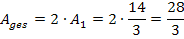
Der gesuchte Flächeninhalt beträgt .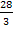

11. Bsp.:Eine Fläche, die sich ins Unendliche erstreckt, aber nicht unendlich großist

Gegeben ist die Funktion 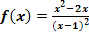mit maximalem Definitionsbereich 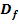. Ihr Graph sei .

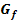a.) Bestimme 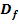und die Schnittpunkte von 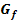mit der x-Achse.

b.) Untersuche das Verhalten von 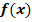an den Rändern des Definitionsbereichs und gib die Gleichungen aller Asymptoten an!

c.) Untersuche das Monotonieverhalten von 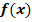und zeige, dass die Funktion kein Extremum hat.

d.) Skizziere den Graph 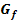unter Berücksichtigung der bisherigen Ergebnisse für 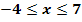in ein Koordinatensystem.

e.) Zeige, dass 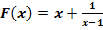eine Stammfunktion von 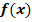ist.

f.) Berechne in Abhängigkeit von u den Inhalt 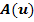des Flächenstücks, das durch 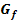und seine waagrechte Asymptote sowie den senkrechten Geraden x = 2 und x = u eingeschlossen wird. Es gilt dabei u >2.

Ermittle dann 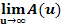und interpretiere das Ergebnis geometrisch-anschaulich!

Lösung:

Zu 11a.)

Gesucht sind in dieser Teilaufgabe die maximale Definitionsmenge und die Schnittpunkte der Funktion 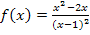mit den Koordinatenachsen.

Definitionsmenge ermitteln:

Bekanntlich ist die Division durch Null nicht definiert. In anderen Worten:Man darf nicht durch Null teilen. Daher darf hier die Zahl 1 nicht für x eingesetzt werden, denn für x = 1 würde sich im Nenner 0 ergeben. Für alle anderen reellen Zahlen ist die Funktion definiert. Somit gilt: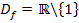

Schnittpunkte mit den Achsen berechnen:

1. Schnittpunkte mit der x-Achse (Nullstellen)

Um die Schnittpunkte einer Funktion mit der x-Achse, d.h. ihre Nullstellen, zu berechnen, muss die Funktion gleich Null gesetzt werden. Jeder Punkt der x-Achse muss schließlich die y-Koordinate y = 0 besitzen. Da nur eine andere Schreibweise für y darstellt, muss bei den Nullstellen gelten: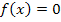

Daher setzen wir die Funktionsgleichung gleich 0 und lösen nach x auf.

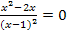
Da ein Bruch nur dann gleich Null sein kann, wenn der Zähler gleich Null ist, setzen wir einfach den Zähler gleich Null. (Wenn du die Gleichung mit dem Nenner multiplizierst, kommst du auf das gleiche, denn dann ergibt sich auf der rechten Seite 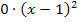und das ist schließlich 0.)

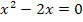
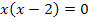
Durch das Ausklammern von x entsteht eine Gleichung der Form „Produkt gleich Null“. Ein Produkt ist bekanntlich gleich Null, wenn einer der Faktoren gleich Null ist. Daher dürfen wir die Faktoren einzeln gleich Null setzen. Die Lösungen lassen sich direkt ablesen:

---