1. Flächenberechnungenmit Hilfe von Integralen

Hier noch einmal die zu lösende Gleichung: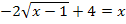

Probe für x = 10: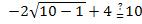

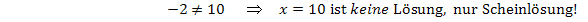
Probe für x = 2: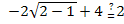

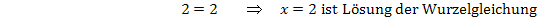
Die Funktion und ihre Umkehrfunktion schneiden sich nur an der Stelle x = 2. Der Wert x = 2 liegt sowohl innerhalb von 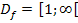als auch in 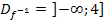. Der andere Wert x = 10 kommt auch deshalb nicht als Schnittpunkt der Funktionen und in Frage, weil x = 10 nicht in der Definitionsmenge 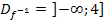liegt.

Nur der Punkt S(2|2) ist gemeinsamer Punkt beider Funktionen.

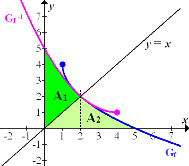
Nun überlegen wir uns, wie wir die gesuchte Fläche zerlegen, damit sie sich besser berechnen lässt. Die Winkelhalbierende muss das gesuchte Flächenstück zwangsläufig halbieren, da die gesuchte Fläche symmetrisch zur Winkelhalbierenden liegt. Die Winkelhalbierende y = x teilt die gesuchte Fläche somit in die zwei gleich großen Flächenstücke und 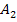. Es reicht demnach aus, wenn wir nur den Inhalt eines dieser beiden Flächenstücke berechnen und das Ergebnis mit 2 multiplizieren. Nun stellt sich die Frage, welches der beiden Flächenstücke leichter zu berechnen ist. Welches würdest du nehmen, das oberhalb oder das unterhalb der Winkelhalbierenden? Bitte erst ´mal selbst darüber nachdenken! Betrachte dazu noch einmal die Abbildung!

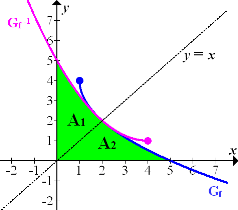
Das Flächenstück , das oberhalb der Winkelhalbierenden liegt, ist die Fläche zwischen der Funktion 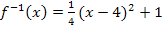und der Winkelhalbierenden y = x von der y-Achse bis zur x-Koordinate des Schnittpunkts x = 2. Es handelt sich also um die Fläche zwischen zwei Funktionen;wir können ihren Inhalt berechnen, indem wir das Integral der oberen minus der unteren Funktion berechnen. Die y-Achse, d.h. x = 0, entspricht der unteren Integrationsgrenze;x = 2 ist obere Grenze. Eine Stammfunktion können wir zu 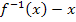lässt sich leicht finden, denn 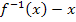ist eine quadratische Funktion.

Das andere Flächenstück 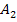, das unterhalb der Winkelhalbierenden liegt, ist nach untenhin begrenzt durch die x-Achse, nach oben teils durch die Winkelhalbierende und teils durch die Wurzelfunktion . Man müsste es an der Stelle x = 2 aufteilen, um deren Flächeninhalt zu berechnen.

Da es jedoch schwieriger ist eine Stammfunktion zu einer Wurzelfunktion zu finden als zu einer quadratischen Funktion, entscheiden wir uns hier für die Berechnung des Flächenstücks , welches oberhalb der Winkelhalbierenden liegt

Berechnung der Fläche 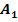(Fläche zwischen 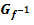, der y-Achse und der Winkelhalbierenden y = x):

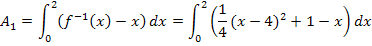
Bevor wir integrieren, vereinfachen wir den Integranden. D.h. wir verwenden die zweite binomische Formel 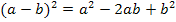, multiplizieren dann den Faktor 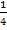in die Klammer hinein und fassen den Ausdruck hinter dem Integral soweit möglich zusammen.

---